We begin with a classical analytic example, from ``Pi, Euler Numbers, and Asymptotic Expansions'' [1].
R. D. North asked for an explanation of the following fact:
The number on the right is not 
to 40 places. As one would expect,
the 6th digit after the decimal point is wrong. The surprise is that only
the underlined digits are wrong. This is explained in detail in [1]. The
discovery of the explanation is quite difficult from this result, but is somewhat
easier from the following similar one:
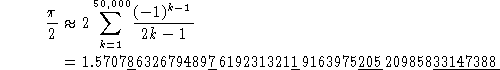
Here we note that if we add 1, -1, 5, and -61 to the incorrect digits,
we get equality (to 40 places) with 
.
With the help of Sloane and Plouffe (or indeed with
the help of Sloane's original Handbook, as was actually the case, or the computer programs) we can identify these
as the first four nonzero Euler numbers. We conjecture, then, that the error is of the form
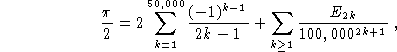
where 
is the 
nonzero Euler number. We can test this conjecture by
computation,
and find by adding the first 80 terms in the error formula above to the
sum that we get to 500 digits. This does not tell us that our conjecture
is true, but at least it encourages us that a proof might be possible.
See [1] for the proof.
The point of this example was that recognition of the Euler numbers in this
at first required ingenuity (to shift from to ,
because the original problem
has twice the Euler numbers appearing in it). However, the case has changed:
the new programs both recognize twice the Euler numbers.
If we do not give enough terms to superseeker, it fails to return
anything (the heuristics of the program are not designed for
short sequences, which, after all, can represent far too many
things to be really useful). If we put in 7 terms, however,
it returns
Report on [ 2,2,10,122,2770,101042,5405530]:
Many tests are carried out, but only potentially useful information
(if any) is reported here.
TEST: APPLY VARIOUS TRANSFORMATIONS TO SEQUENCE AND LOOK IT
UP IN THE ENCYCLOPEDIA AGAIN
SUCCESS
(limited to 10 matches):
Transformation T003 gave a match with sequence A0364
Transformation T004 gave a match with sequence A0364
List of sequences mentioned:
%I A0364 M4019 N1667
%S A0364 1,1,5,61,1385,50521,2702765,199360981,19391512145,2404879675441,
%T A0364 370371188237525,69348874393137901,15514534163557086905,
%U A0364 4087072509293123892361
%N A0364 Euler numbers: expansion of sec $x$ .
%R A0364 AS1 810. MOC 21 675 67.
<some cryptic material omitted>
References (if any):
[AS1] = M. Abramowitz and I. A. Stegun, { Handbook of Mathematical
Functions}, National Bureau of Standards, Washington DC, 1964.
[MOC] = { Mathematics of Computation} (formerly { Mathematical Tables and
Other Aids to Computation}).
List of transformations used:
T003 sequence divided by the gcd of its elements
T004 sequence divided by the gcd of its elements, from the 2nd term
Abbreviations used in the above list of transformations:
u[j] = j-th term of the sequence
v[j] = u[j]/(j-1)!
Sn(z) = ordinary generating function
En(z) = exponential generating function
The Euler numbers appear as sequence M4019 in the book. [The code here is to the explicit tag in the book; A0364 is an internal absolute code while T003 tags the transformation used.]