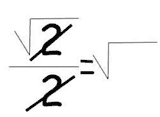An Irrational Proof
The proof that √2 is irrational is fairly simple, but has big implications for how we think about numbers. Hippasus may have been killed for his geometric proof, so here we’ll stick to an algebraic one.
The Proof
Assume that √2 is rational.
This means it can be expressed as m/n, where m and n are integers. Let m/n be in reduced form. This means that m and n have no common factors.
√2=m/n
√2n=m
2n2=m2
Since 2 times an integer equals m2, m2 must be even. (If 2 times an integer equals
Since m2 is even, m must be even. (If m ws odd then m2 would be odd, since multiplying two odd numbers together alwys makes another odd number.)
This means we can express m as 2k (where k is any integer).
We plug 2k into the equation:
2n2=(2k)2
2n2=4k2
n2=2k2
This means n2 is even, so n is even.
So we can express n as 2j (where j is any integer).
√2=m/n
√2=2k/2j
HEY! THAT"S NOT REDUCED!
At the start of the proof we said that m/n expressed √2 in reduced form. If m/n=2k/2j then m and n have the common factor 2, so clearly the fraction isn't reduced.
Our assumption led to a contradiction, so it must be wrong.
√2 cannot be rational.
√2 is irrational.