Playing with Infinity
We know that
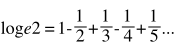
This is an infinite sum much like Madelungs constant. But what if we add the terms in a different order?
Shocking Results
Normally this would be no big deal; adding the numbers 3, 7, and -4 would always give 6 no matter what order you chose to add them in. The key difference is that 3+7-4 is a finite sum, but the series we are rearranging is an infinite sum. Let's try shifting things around a bit.
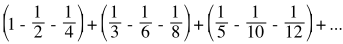
![=sum[k=1->∞] 1/(2k-1) - 1/(4k-2) - 1/(4k)](../../images/content/eq_inf_2.png)
![=sum[k=1->∞] 1/(4k(2k-1))](../../images/content/eq_inf_3.png)
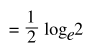
We have made the same set of numbers add up to half of what we had before. In fact, we can make the sum add to any number we wish in the following manner.
Expanding the Example
Suppose we wish to have the sum add to 2. We start by adding positive terms. 1+1/3+1/5+1/7+...+1/15 to get a number just above 2 (around 2.02). Then we start use the negative terms to dip below 2. We only need to subtract 1/2 to get around 1.52. Then we continue adding more positive terms 1/17+1/19...etc until we get above 2 again. Then we use 1/4 to dip back down, and so forth.
We end up using all the numbers, and the sum bobs up and down getting closer and closer to 2 the farther we go towards infinity. Note that there is nothing special about 2, because we can substitute any other number use the same method.
Riemann Series Theorem
The series that we examined above is called a conditionally convergent series. This is a summed series of numbers that normally converges, but if we make all the terms positive it diverges. In the above example, if we make all the terms positive, then it becomes the divergent harmonic series. A conditionally convergent series will always have an infinite number of both positive and negative terms.
Now here is where it gets really strange; our example is not just an isolated fluke. By rearranging the order in which we add the terms, we can make any conditionally convergent series sum to any real number we want or have it diverge off to infinity. This is called the Riemann Series Theorem, developed by the same mathematician that is responsible for the Riemann Hypothesis.
If your mind is swimming with outrage and uncertainty right now, you're not alone. Fortunately, there is some comfort available. Given an infinite sum in mathematics, the order in which you add the terms is usually defined so that there only one answer to the sum.
Reconsidering Madelung
As we saw on the main page, Madelung's constant is defined as:
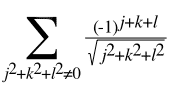
The interesting part about this definition is that it tells us what to add but not what order to add it in.
The definition of Madelung's constant is a conditionally convergent series, so by the Riemann Series Theorem, we can make it add up to which ever number we wish. That's horrible! It's not really a constant if we can make it what ever value we want it to be.

Avoiding Disaster
But don't you worry, because there is one thing here that we are forgetting: the sum is a mathematical model of nature. If you actually look at salt crystals up close, they don't look wavy or spherical. Salt crystals come in cubes, rectangles, and very jagged pieces. This is because salt likes to be electrically neutral, with approximately the same number of positive charges and negative charges. Because of this, salt is only going to form in certain ways. We have an extra constraint on our model.
This is why the method of expanding cubes works so well when we are calculating Madelung's constant. We add up the charges in the same way that they wish to be added in nature. This way, the derived value is a legitimate reflection of the experimental value.




