Chapter 6 CA6: The Directional Derivative
We have noted previously that the instantaneous rate of change of a function \(z = f(x,y)\) at the point \((x,y) = (x_0,y_0)\) will depend on the direction in which the independent variables are changing.
Example 6.0.1.
Consider the function \(f(x,y) = x^2-y^2\text{.}\) The graph of this function is shown below. At \((x,y)=(0,0)\text{,}\) \(f=0\text{.}\) As we can see by looking at the graph, as we move away from the origin along the positive \(x\)-axis the value of \(f\) is increasing, i.e. the rate of change of the function will be positive. However, if we move away from the origin along the positive \(y\)-axis the value of \(f\) is decreasing, i.e. the rate of change of the function will be negative.
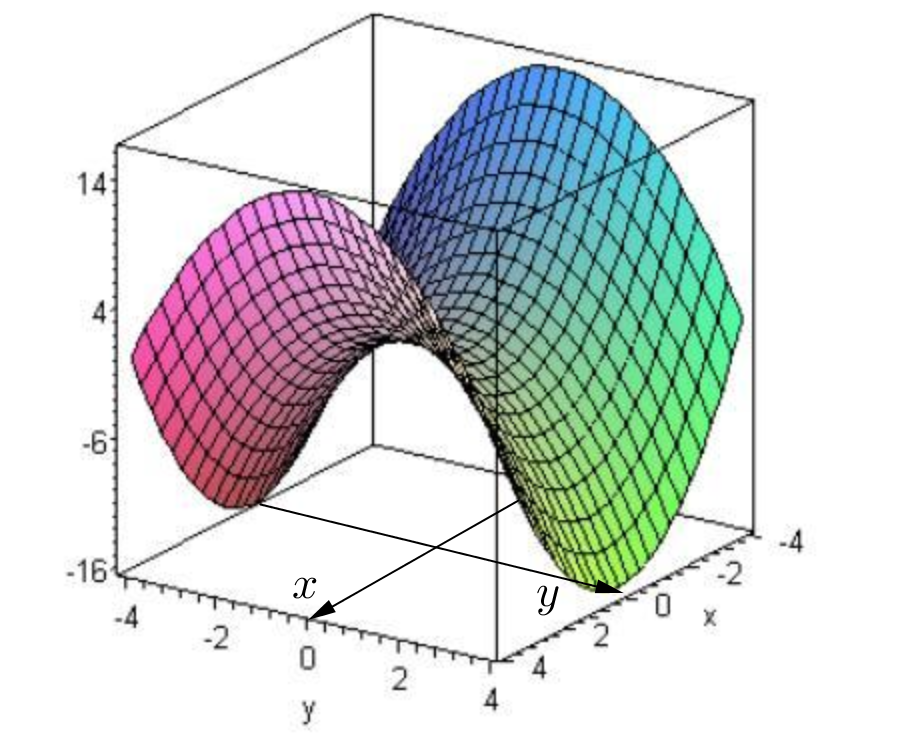
In the case that the direction is parallel to the positive x-axis we already know that the slope is given by the partial derivative \(f_x(x_0,y_0)\) and in the case that the direction is parallel to the positive \(y\)-axis the slope is given by \(f_y(x_0,y_0)\text{.}\) In this section we will look at the problem of finding the slope of the function if we move away from the point \((x,y) = (x_0,y_0)\) in any direction.