Section 7.2 Second Derivative Test
An algebraic method for determining what type of critical points a function has is given by the following theorem.
Theorem 7.2.1. The Second Derivative Test.
Let the function \(z=f(x,y)\) have continuous 2nd partial derivatives and let \((x_0,y_0)\) be a critical point of the function. Let
If \(D>0\) and \(f_{xx} (x_0,y_0) >0\) then \(f\) has a local minimum at \((x_0,y_0)\text{.}\)
If \(D>0\) and \(f_{xx} (x_0,y_0) < 0\) then \(f\) has a local maximum at \((x_0,y_0)\text{.}\)
If \(D < 0\) then \(f\) has a saddle point at \((x_0,y_0)\text{.}\)
If \(D=0\) then the 2nd derivative test is inconclusive.
Outline of Proof.
For the sake of simplicity assume that the critical point is at the point \((x_0,y_0)=(0,0)\text{.}\) Now using a Taylor expansion for functions of two variables about \((a,b) = (0,0)\) we have (up to the quadratic terms)
Since \((x_0,y_0) = (0,0)\) is a critical point of the function \(f_x (0,0) = f_y (0,0) = 0\text{.}\) Thus
On completing the square (and dropping the evaluation at \((0,0)\) for brevity)
From this we can see that if \(f_{xx} > 0\) and \(D = f_{xx} f_{yy} - f_{xy}^2 > 0\) then when \(x\) and \(y\) are varied from \((0,0)\text{,}\) \(f(x,y)\) increases and so \((x_0,y_0) = (0,0)\) will be a local minimum.
Example 7.2.2.
Locate and identify the critical points of the function \(f(x,y) = 2x^3 + (x+1)y^2 + 5x^2\text{.}\)
\(\left(0,0\right)\) is a local minimum; \(\left(-\dfrac{5}{3},0\right)\) is a local maximum; \(\left(-1,2\right)\) and \(\left(-1,-2\right)\) are saddle points.
We located the critical points of this function in an earlier example. We found that there are 4 critical points at
To determine the nature of these critical points, in this example we will use the second derivative test. To this end, note that
Thus
Now, applying the second derivative test:
At \((0,0)\text{,}\) \(D=20>0\text{,}\) \(f_{xx}=10>0\) and so \((0,0)\) is a local minimum.
At \((-\dfrac{5}{3},0)\text{,}\) \(D=\dfrac{40}{3}>0\text{,}\) \(f_{xx}=-10 < 0\) and so \((-\dfrac{5}{3},0)\) is a local maximum.
At \((-1,2)\text{,}\) \(D=-16 < 0\) and so \((-1,2)\) is a saddle point.
At \((-1,-2)\text{,}\) \(D=-16 < 0\) and so \((-1,-2)\) is also a saddle point.
This is in agreement with the conclusions we made on the nature of these critical pointson the basis of the level curves of the function.
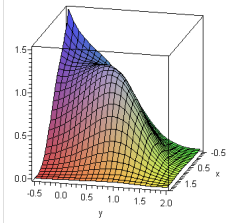
Example 7.2.3.
Locate and identify the critical points of the function
\((0,0)\) is a local maximum.
Here
For this function both partial derivatives are undefined at \((x, y) = (0,0)\) and so this point will be a critical point. However we cannot use the second derivative test to determine the nature of this critical point. In this case we can see from the graph of the function that the critical point at \((x, y) = (0,0)\) is a local maximum.
Exercises Example Tasks
1.
Locate and identify the critical points of the function \(z=3x-x^3-2y^2+y^4\text{.}\)
2.
Locate and identify the critical points of the function \(z=\exp \left(xy-\frac{2}{3}x^3 - \frac{2}{3}y^3 \right)\text{.}\)