Section 19.1 Introduction
Definition 19.1.1.
Let A be a square matrix of order \(n\text{.}\) The scalar \(\lambda\) is called an eigenvalue of \(A\) if there is a non-zero vector \(\mathbf{x}\) for which
\(\mathbf{x}\) is called an eigenvector of \(A\) associated with the eigenvalue \(\lambda\text{.}\)
Example 19.1.2.
For the matrix
determine if any of \(\mathbf{x}=\begin{pmatrix} 18 \amp 6 \amp 1 \end{pmatrix}^T \text{,}\) \(\mathbf{y}=\begin{pmatrix} -2 \amp 3 \amp 4 \end{pmatrix}^T \) or \(\mathbf{z}=\begin{pmatrix} 36 \amp 12 \amp 2 \end{pmatrix}^T \) are eigenvectors of \(A\text{.}\)
Answer.\(\mathbf{x}\) and \(\mathbf{z}\) are eigenvectors of \(A\text{.}\)
Since
\(\mathbf{x}\) is an eigenvector of \(A\) associated with the eigenvalue \(\frac{3}{2}\text{.}\) Since
\(\mathbf{y}\) is not an eigenvector of \(A\text{.}\) Since
\(\mathbf{z}\) is also an eigenvector of \(A\) associated with the eigenvalue \(\frac{3}{2}\text{.}\)
Example 19.1.3.
The matrix
is the matrix for the plane transformation of a reflection in the line \(y=x\text{.}\) Use this geometric interpretation of the matrix to determine the possible eigenvectors and eigenvalues of \(A\text{.}\)
Answer.\(\mathbf{x}=t\begin{pmatrix} 1 \\ 1 \end{pmatrix}, \textrm{ where } t\in \mathbb{R}\) with eigenvalue \(1\text{.}\)
\(\mathbf{x}=t\begin{pmatrix} 1 \\ -1 \end{pmatrix}, \textrm{ where } t\in \mathbb{R}\) with eigenvalue \(-1\text{.}\)
By definition eigenvectors satisfy the equation
Thinking in terms of transformations this equation says that an eigenvector will be a vector that is mapped by the transformation to some scalar multiple of itself, (i.e. to a vector parallel to itself). As illustrated in Figure 19.1.4 any vector lying on the line \(y=x\) will be mapped to itself by a reflection in that line, i.e. for such vectors
Thus vectors of the form
will be eigenvectors of \(A\) with an eigenvalue of \(1\text{.}\) (Note that we could check this algebraically if so desired.)
As also illustrated in Figure 19.1.4, any vector perpendicular to the line \(y=x\) will be mapped by a reflection in that line to a vector of the same length but in the opposite direction, i.e. for such vectors
Thus vectors of the form
will be eigenvectors of \(A\) with an eigenvalue of \(-1\text{.}\) 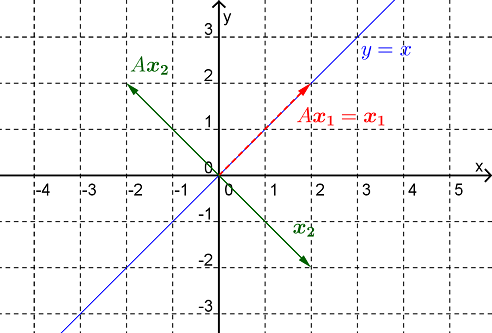
Example 19.1.5.
Given that \(\lambda=5\) is an eigenvalue for the matrix
find all eigenvectors associated with this eigenvalue.
Answer.The eigenvectors associated with the eigenvalue \(\lambda=5\) are all scalar multiples of the vector \(\begin{pmatrix} 1 \amp 2 \end{pmatrix}^T\text{.}\)
An eigenvector, \(\mathbf{x}\text{,}\) associated with the eigenvalue \(\lambda=5\) will satisfy the system of linear equations
which can be rewritten as
Now, using Gauss Jordon elimination to solve this homogeneous system
we see that this system has an infinite number of solutions which take the form
or equivalently
Thus the eigenvectors associated with the eigenvalue \(\lambda=5\) are all scalar multiples of the vector \(\begin{pmatrix} 1 \amp 2 \end{pmatrix}^T\text{.}\)
Of course, it is a good idea to check this result. Since
it is correct.