Tangent Planes

Section 5.1 Tangent Planes

Recall that the graph associated with the function

z = f (x, y)

is a surface in

R^{3}

(that passes the vertical line test). Wherever this surface does not have any discontinuities or cusp-like points it will have a tangent plane. Like the tangent line to the graph of a function of one variable, the tangent plane to the function

z = f (x, y)

at the point

(x_{0}, y_{0})

is the plane that “just touches” the surface at the point

(x_{0}, y_{0}, z_{0}) .

🔗

Example 5.1.1.

For the function $f (x, y) = 5 - \frac{x^{2} + y^{2}}{2}$ the graph below shows the graph of the function and it's tangent plane at the point $(x, y) = (2, 1) .$

🔗

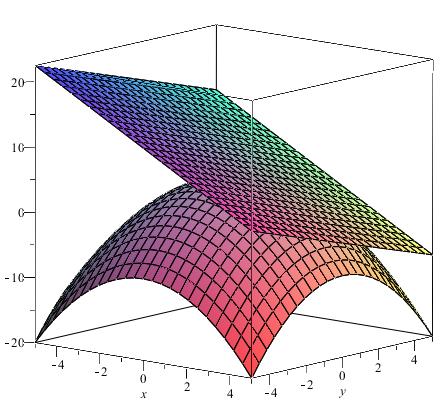
To find the equation of the plane tangent to the function

z = f (x, y)

at the point

(x_{0}, y_{0}, z_{0}),

firstly recall that the equation of a plane in Cartesian form is given by

a x + b y + c z = k, a, b, c, k \in R,

🔗

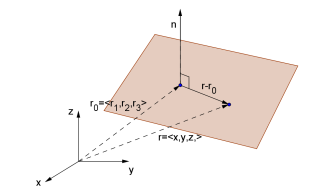
or in normal form, as illustrated in Figure 5.1.3, by

\begin{matrix} (5.1.1) & n \cdot (r - r_{0}) = 0 \end{matrix}

🔗

where

n = ⟨ a, b, c ⟩

is a normal vector to the plane,

r_{0}

is the position vector of a point on the plane and

r = ⟨ x, y, z ⟩ .

🔗

Example 5.1.4.

Find the equation of the tangent plane to the function $f (x, y) = 5 - \frac{x^{2} + y^{2}}{2}$ at $(x, y) = (2, 1) .$

Answer.

$2 x + y + z = \frac{15}{2}$

Solution.

Now, we know that the partial derivative $f_{x} (2, 1)$ gives the slope of the tangent at $x = 2,$ to the curve of intersection of the surface associated with $f$ and the plane $y = 1 .$

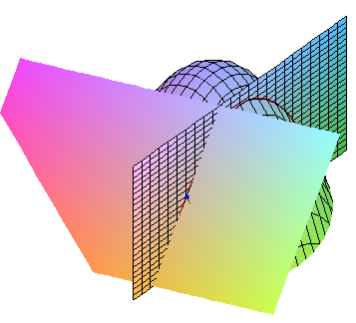
Since this tangent line lies in the plane tangent to $f$ at $(x, y) = (2, 1)$ the vector

⟨ 1, 0, f_{x} (2, 1) ⟩

will be a vector that is parallel to the tangent plane, (or lies in the tangent plane if we place it’s tail at the point $(2, 1, \frac{5}{2})$ ). Similarly, the vector

⟨ 0, 1, f_{y} (2, 1) ⟩

will be another vector parallel to the tangent plane. Since these two non-parallel vectors are parallel to the tangent plane, their vector product will give a vector normal to the tangent plane, i.e.

\begin{aligned} n & = ⟨ 1, 0, f_{x} (2, 1) ⟩ \times ⟨ 0, 1, f_{y} (2, 1) ⟩ \\ = ⟨ - f_{x} (2, 1), - f_{y} (2, 1), 1 ⟩ \\ = ⟨ 2, 1, 1 ⟩ \end{aligned}

Thus, using equation (5.1.1), the equation of the plane tangent to $f (x, y) = 5 - \frac{x^{2} + y^{2}}{2}$ at $(x, y) = (2, 1)$ is

⟨ 2, 1, 1 ⟩ \cdot (⟨ x, y, z ⟩ - ⟨ 2, 1, \frac{5}{2} ⟩) = 0

which simplifies to

2 x + y + z = \frac{15}{2} .

🔗

In general, to find the equation of the plane tangent to the function

f (x, y)

at the point

(x_{0}, y_{0}),

note that the vectors

⟨ 1, 0, f_{x} (x_{0}, y_{0}) ⟩ and ⟨ 0, 1, f_{y} (x_{0}, y_{0}) ⟩

🔗

lie in the tangent plane and hence a normal to the plane is

\begin{aligned} n & = ⟨ 1, 0, f_{x} (x_{0}, y_{0}) ⟩ \times ⟨ 0, 1, f_{y} (x_{0}, y_{0}) ⟩ \\ = ⟨ - f_{x} (x_{0}, y_{0}), - f_{y} (x_{0}, y_{0}), 1 ⟩ . \end{aligned}

🔗

Since the point

(x_{0}, y_{0}, z_{0})

lies on the plane, using equation (5.1.1), the equation of the tangent plane is

⟨ - f_{x} (x_{0}, y_{0}), - f_{y} (x_{0}, y_{0}), 1 ⟩ \cdot (⟨ x, y, z ⟩ - ⟨ x_{0}, y_{0}, z_{0} ⟩) = 0.

🔗

On expanding and rearranging this we get the following result.

🔗

Theorem 5.1.6.

The equation of the plane tangent to the function $f (x, y)$ at the point $(x_{0}, y_{0}, z_{0})$ is

z = z_{0} + f_{x} (x_{0}, y_{0}) (x - x_{0}) + f_{y} (x_{0}, y_{0}) (y - y_{0}),

where $z_{0} = f (x_{0}, y_{0}) .$

🔗

Example 5.1.7.

Find the equation of the plane tangent to $z = x^{2} + 2 y^{2}$ at the point $(x, y) = (1, 2) .$

Answer.

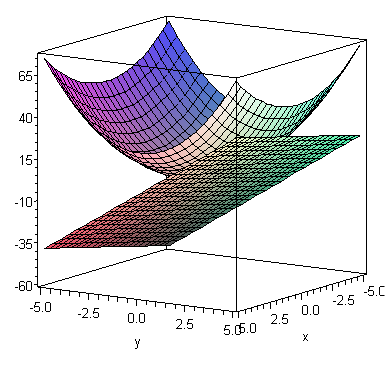
$2 x + 8 y - z - 9 = 0$

Solution.

Firstly, note that when $(x, y) = (1, 2),$ $z = 9 .$ Now

z_{x} = 2 x and so z_{x} (1, 2) = 2

and

z_{y} = 4 y and so z_{y} (1, 2) = 8 .

Thus the equation of the tangent plane is

z = 9 + 2 (x - 1) + 8 (y - 2)

which simplifies to

2 x + 8 y - z - 9 = 0 .

🔗

Example 5.1.9.

Find the equation of the line normal to the graph of the function $z = x^{2} + 2 y^{2}$ at the point $(x, y) = (1, 2) .$

Answer.

$r = ⟨ 1, 2, 9 ⟩ + t ⟨ - 2, - 8, 1 ⟩$

Solution.

Recall that the vector equation of a line in $R^{3}$ is

r = r_{0} + t d, t \in R

where $r = ⟨ x, y, z ⟩$ is the position vector of a general point, $r_{0}$ is the position vector of a point that lies on the line and $d$ is a direction vector for the line (i.e. a vector that is parallel to the line).

We know that a vector normal to the surface $z = f (x, y)$ at the point $(x_{0}, y_{0}, z_{0})$ is given by

n = ⟨ - f_{x} (x_{0}, y_{0}), - f_{y} (x_{0}, y_{0}), 1 ⟩ .

For the function $z = x^{2} + 2 y^{2},$ $z_{x} = 2 x$ and $z_{y} = 4 y .$ Thus a direction vector for the line normal to $z = x^{2} + 2 y^{2}$ at the point $(x, y) = (1, 2)$ will be

d = ⟨ - 2, - 8, 1 ⟩ .

Since the normal line passes through the point $(1, 2, 9)$ its equation is

r = ⟨ 1, 2, 9 ⟩ + t ⟨ - 2, - 8, 1 ⟩ .

🔗

Exercises Example Tasks

🔗

1.

Find the equation of the tangent plane to $z = x^{2} - 5 x y + 2 y^{2}$ at the point $(x, y) = (- 1, - 2) .$

🔗

2.

Find the equation of the tangent plane and normal line to $z = \sqrt{x + y} \sin (x y)$ at the point $(x, y) = (0, 1) .$

🔗

3.

Show that every line that is normal to the sphere $x^{2} + y^{2} + z^{2} = 1$ passes through the origin.