Skip to main content

Section 1.3 Maclaurin Series

In this section we will discuss the task of finding an infinite series representation for a given function of one variable, \(f\text{.}\) We begin by assuming that the given function \(f(x)\) does indeed have a power series representation, at least initially about \(x=0\text{.}\) Thus we assume that on some interval \(|x| < R\)

\begin{equation} f(x) = \sum_{k=0}^{\infty}c_kx^k = c_0 + c_1x +c_2x^2 +c_3x^3 + \cdots.\label{Eq-Maclaurin_of_f}\tag{1.3.1} \end{equation}

We know that the power series reduces to \(c_0\) when \(x=0\) and so for the power series to match the function when \(x=0\) we must have \(c_0 = f(0)\text{.}\) On differentiating (1.3.1) we get

\begin{equation} f'(x) = \sum_{k=1}^{\infty}kc_kx^{k-1} = c_1 +2c_2x +3c_3x^2 + 4c_4x^3 + \cdots\label{Eq-First_derivative_Maclaurin}\tag{1.3.2} \end{equation}

and on putting \(x=0\) into this gives \(c_1=f'(0)\text{.}\) Similarly, differentiating (1.3.2)

\begin{equation} f''(x) = \sum_{k=2}^{\infty}k(k-1)c_kx^{k-2} = 2c_2 +6c_3x + 12c_4x^2 + \cdots\tag{1.3.3} \end{equation}

and substituting \(x=0\) gives \(c_2=\dfrac{1}{2}f''(0)\text{.}\) By continuing this process, we can see that in general

\begin{equation} f^{(n)}(x) = \sum_{k=n}^{\infty}k(k-1)(k-2)\cdots(k-(n-1))c_kx^{k-n}\tag{1.3.4} \end{equation}

and hence (by substituting \(x=0\)) that \(c_n = \dfrac{1}{n!}f^{(n)}(0)\text{.}\)

Definition 1.3.1. Maclaurin Series.

The series

\begin{equation*} \sum_{k=0}^{\infty}\dfrac{f^{(k)}(0)}{k!}x^k = f(0) + f'(0)x +\dfrac{f^{''}(0)}{2!}x^2 +\dfrac{f^{'''}(0)}{3!}x^3 + \cdots \end{equation*}

is called the Maclaurin series for \(f(x)\text{.}\)

We know that the Maclaurin series for \(f\) converges when \(x=0\) (since all power series converge for \(x=a\)) and we also know that the series converges to \(f(0)\) (because we constructed it that way). However for other values of \(x\) we cannot be sure that the infinite series will converge and if it does, does it converge to the function value.

Find the Maclaurin series for \(f(x)=\dfrac{1}{1-x}\text{.}\)

Answer.

\(\displaystyle \sum_{k=0}^{\infty}x^k = 1+x+x^2+x^3+x^4+ \cdots\)

Solution.

Firstly find the derivatives of \(f\) and evaluate them at \(x=0\text{.}\)

\begin{alignat*}{1} f(x) \amp = (1-x)^{-1} \text{ and hence } f(0)=1\\ f'(x) \amp = (1-x)^{-2} \text{ and hence } f'(0)=1\\ f''(x) \amp = 2(1-x)^{-3} \text{ and hence } f''(0)=2\\ \quad\amp \vdots \quad \\ f^{(k)}(x) \amp = k!(1-x)^{-k-1} \text{ and hence } f^{(k)}(0) = k! \end{alignat*}

Substituting these results into the formula derived above gives the Maclaurin series for \(f\) as

\begin{equation*} \sum_{k=0}^{\infty}\dfrac{k!}{k!}x^k = \sum_{k=0}^{\infty}x^k = 1+x+x^2+x^3+x^4+ \cdots. \end{equation*}

This agrees with the result that we found in an earlier example. As we saw in that example, however, the Maclaurin series only converges for \(|x| <1 \) and that for those values it converges to the function value.

Definition 1.3.3. Maclaurin Polynomial.

The \(n\)th partial sum of the Maclaurin series for \(f(x)\text{,}\) i.e.,

\begin{equation*} \sum_{k=0}^{n}\dfrac{f^{(k)}(0)}{k!}x^k = f(0) + f'(0)x +\dfrac{f^{''}(0)}{2!}x^2 +\cdots + \dfrac{f^{(n)}(0)}{n!}x^n \end{equation*}

is called the Maclaurin polynomial of degree \(n\) for \(f(x)\text{.}\)

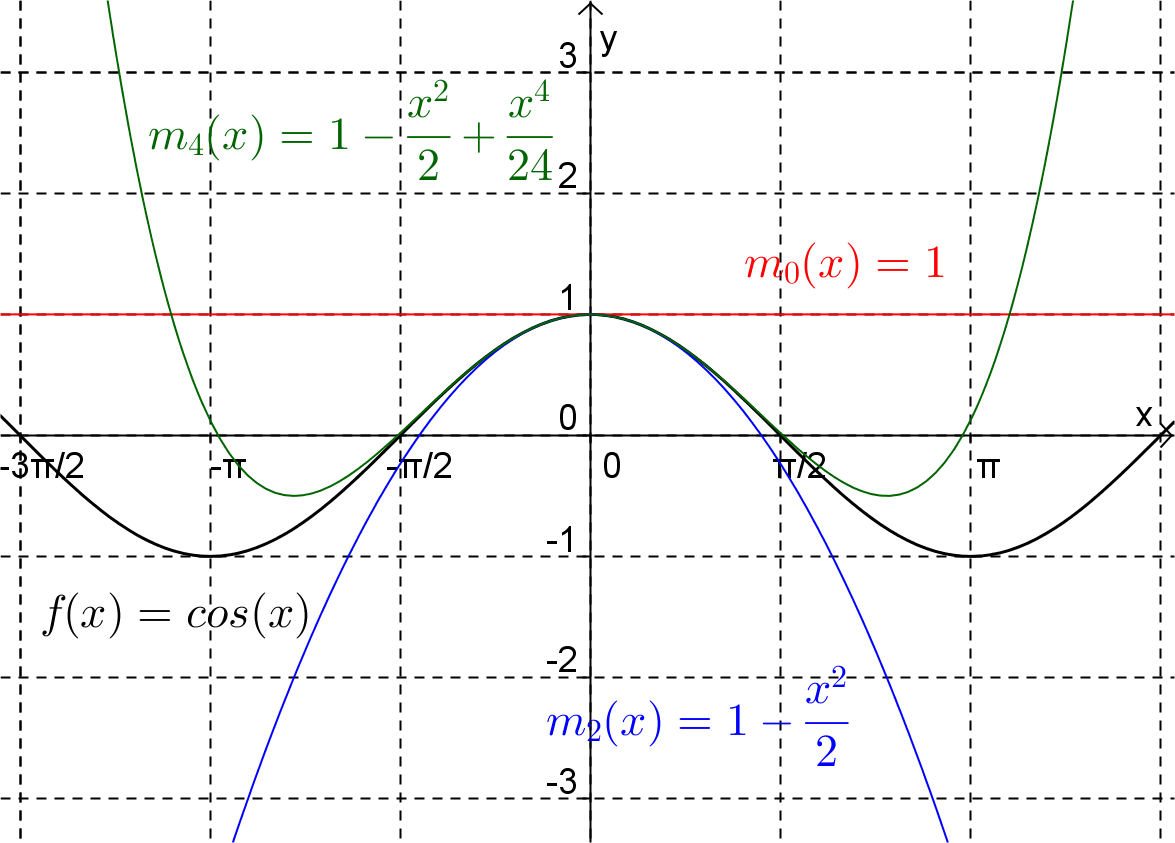
Find the Maclaurin polynomials of degree \(0,1,2,3\) and \(4\) for the function \(f(x)=\cos(x)\text{.}\)

Answer.
\begin{align*} M_0(x)\amp=1\\ M_1(x)\amp=1\\ M_2(x)\amp=1-\dfrac{x^2}{2}\\ M_3(x)\amp=1-\dfrac{x^2}{2}\\ M_4(x)\amp=1-\dfrac{x^2}{2}+\dfrac{x^4}{24} \end{align*}
Solution.

For \(f(x)=\cos(x)\text{,}\)

\begin{alignat*}{1} f(x) \amp = \cos(x) \text{ and hence } f(0)=1\\ f'(x) \amp = -\sin(x) \text{ and hence } f'(0)=0\\ f''(x) \amp = -\cos(x) \text{ and hence } f''(0)=-1\\ f'''(x) \amp = \sin(x) \text{ and hence } f'''(0)=0\\ f^{(iv)}(x) \amp = \cos(x) \text{ and hence } f^{(iv)}(0)=1 \end{alignat*}

and so the \(0\)th degree Maclaurin polynomial is

\begin{equation*} M_0(x)=f(0)=1. \end{equation*}

Notice that the \(0\)th degree Maclaurin polynomial is the horizontal line passing through the point \((0,f(0))\text{.}\)

The \(1\)st degree Maclaurin polynomial is

\begin{alignat*}{1} M_1(x) \amp = f(0) + f'(0)x\\ \amp = 1+0\\ \amp = 1 \end{alignat*}

Notice that the \(1\)st degree Maclaurin polynomial is the tangent to the function at the point \((0,f(0))\text{.}\) Notice also, that in this case, the \(0\)th degree and the \(1\)st degree Maclaurin polynomials are the same.

The \(2\)nd degree Maclaurin polynomial is

\begin{alignat*}{1} M_2(x) \amp = f(0) + f'(0)x + \dfrac{f''(0)}{2}x^2\\ \amp = 1+0x + \dfrac{(-1)}{2}x^2\\ \amp = 1-\dfrac{x^2}{2} \end{alignat*}

The \(3\)rd degree Maclaurin polynomial is

\begin{alignat*}{1} M_3(x) \amp = f(0) + f'(0)x + \dfrac{f''(0)}{2}x^2 + \dfrac{f'''(0)}{3!}x^3\\ \amp = 1+0x + \dfrac{(-1)}{2}x^2 + \dfrac{0}{3!}x^3\\ \amp = 1-\dfrac{x^2}{2} \end{alignat*}

The \(4\)th degree Maclaurin polynomial is

\begin{alignat*}{1} M_4(x) \amp = f(0) + f'(0)x + \dfrac{f''(0)}{2}x^2 + \dfrac{f'''(0)}{3!}x^3 + \dfrac{f^{(iv)}(0)}{4!}x^4\\ \amp = 1+0x + \dfrac{(-1)}{2}x^2 + \dfrac{0}{3!}x^3 + \dfrac{1}{4!}x^4\\ \amp = 1-\dfrac{x^2}{2} + \dfrac{x^4}{24} \end{alignat*}

As can be seen in Figure 1.3.5, in this case as the degree of the Maclaurin polynomial increases so the polynomial provides a good approximation to the function for a larger interval surrounding \(x=0\text{.}\) In fact, using the Ratio test we can show that the Maclaurin series for \(\cos(x)\) converges for all values of \(x\) and by using some more advanced mathematics we can show that the series converges to \(\cos(x)\) for all values of \(x\text{.}\)

Figure 1.3.5.

Exercises Example Tasks

1.

Let \(f(x)=e^x\text{.}\) Find the Maclaurin series for \(f\) and find its interval of convergence.

2.

Find the Maclaurin polynomial of degree \(3\) for \(g(x) = \tan^{-1}(x)\text{.}\)

Remark 1.3.6. Aside.

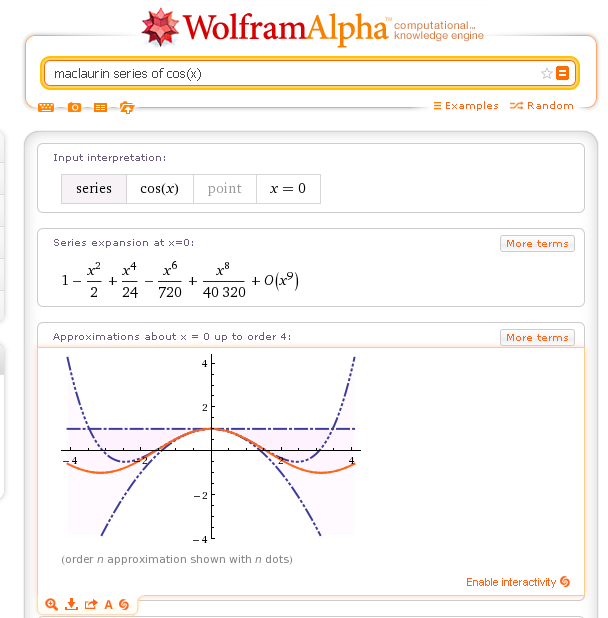
Computer Algebra Systems usually have a command for calculating Maclaurin series. For example, the following shows part of the output from a Wolfram Alpha query.

Figure 1.3.7.