Skip to main content

Section 2.2 Taylor Series

Maclaurin series are power series about \(x=0. \) However we can follow exactly the same process to find a power series expansion for a function \(f(x) \) about any point \(x=a. \) We call these power series Taylor Series.

Definition 2.2.1. Taylor Series.

The series,

\begin{equation*} \sum_{k=0}^{\infty}\dfrac{f^{(k)}(a)}{k!}(x-a)^k=f(a)+f'(a)(x-a)+\dfrac{f''(a)}{2!}(x-a)^{2}+\dfrac{f'''(a)}{3!}(x-a)^3+ \dots \text{.} \end{equation*}

is called the Taylor series for \(f(x) \) about \(x=a. \)

Note that:

  1. We can construct the Taylor series about \(x=a. \) for any function that is infinitely differentiable at \(x=a. \)

  2. The Taylor series for \(f\) about \(x=a \) always converges to \(f(a)\) at \(x=a. \)

  3. If the Taylor series converges for other values of \(x \) these will be in an interval centred on \(x=a. \)

  4. It is possible that a Taylor series may converge to a value other than the function value.

  5. A Maclaurin series is just a Taylor series about \(x=0. \)

  6. The \(n^{\text{th}} \) partial sum of the Taylor series for \(f \) about \(x=a \) is called the \(n^{\text{th}} \) degree Taylor polynomial for \(f \) about \(x=a. \)

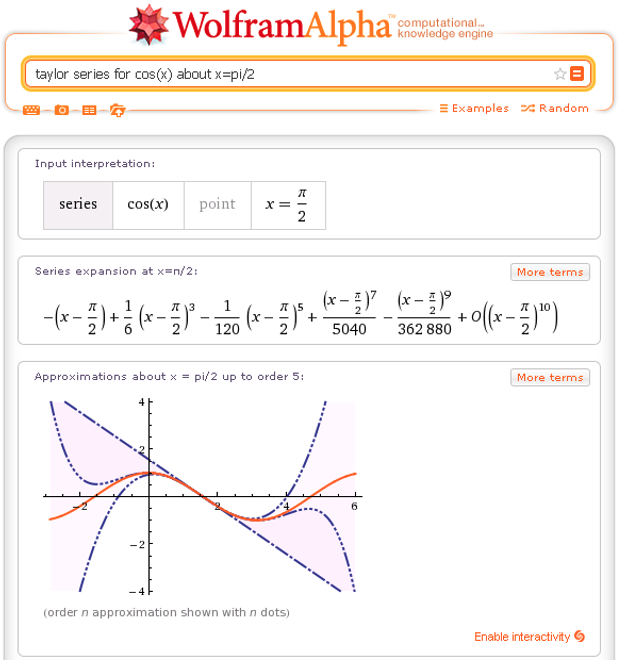
Find the Taylor series for \(f(x)=\cos(x) \) about \(x=\frac{\pi}{2} \)

Answer.

\(\displaystyle\sum_{k=1}^{\infty}(-1)^{k}\dfrac{(x-\frac{\pi}{2})^{2k-1}}{(2k-1)!}\)

Solution.

In order to find the Taylor series for \(f(x)=\cos(x) \) about \(x=\frac{\pi}{2} \) we need to evaluate \(f \) and its derivatives at \(x=\frac{\pi}{2}. \) So,

\begin{align*} f(x) \amp =\cos(x) \,\, \text{and hence}\,\, f\left(\frac{\pi}{2}\right)=0 \\ f'(x) \amp =-\sin(x) \,\, \text{and hence}\,\, f'\left(\frac{\pi}{2}\right)=-1 \\ f''(x) \amp =-\cos(x) \,\, \text{and hence}\,\, f''\left(\frac{\pi}{2}\right)=0 \\ f'''(x) \amp =\sin(x) \,\, \text{and hence}\,\, f'''\left(\frac{\pi}{2}\right)=1 \\ \amp \hspace{5.5cm} \vdots \\ \amp \hspace{4.6cm} f^{(k)}\left(\frac{\pi}{2}\right)=\begin{cases} 0 \amp k\;\, \text{even} \\ (-1)^{\frac{k+1}{2}} \amp k \;\, \text{odd} \end{cases} \end{align*}

Thus the Taylor series for \(f(x)=\cos(x) \) about \(x=\frac{\pi}{2} \) is

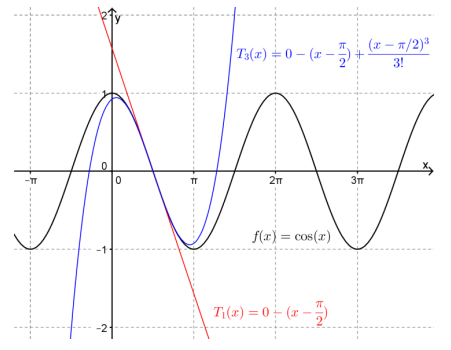
\begin{align*} \amp = 0-(x-\frac{\pi}{2})+0+\frac{1}{3!}(x-\frac{\pi}{2})^{3}-\frac{1}{5!}(x-\frac{\pi}{2})^{5}+\dots\\ \amp =-(x-\frac{\pi}{2})+\frac{(x-\frac{\pi}{2})^{3}}{3!}-\frac{(x-\frac{\pi}{2})^{5}}{5!}+\dots\\ \amp = \sum_{k=1}^{\infty}(-1)^{k}\dfrac{(x-\frac{\pi}{2})^{2k-1}}{(2k-1)!}. \end{align*}

It turns out that this series converges to \(f(x)=\cos(x) \) for all values of \(x. \) Figure 2.2.3 shows the graph of \(f(x)=\cos(x) \) and the Taylor polynomials of degree \(1 \) and degree \(3 \) about \(x=\frac{\pi}{2} .\)

Figure 2.2.3.

Find the second order approximation to \(f(x)=e^{-\frac{x}{3}} \) about \(x=2. \)

Answer.

\(T_{2}(x)=e^{-\frac{2}{3}}-\dfrac{1}{3}e^{-\frac{2}{3}}(x-2)+\dfrac{1}{18}e^{-\frac{2}{3}}(x-2)^{2}\)

Solution.

In order to find the second order approximation for \(f(x)=e^{-\frac{x}{3}} \) about \(x=2 \) we need to evaluate \(f \) and its first two derivatives at \(x=2\text{.}\) So,

\begin{align*} f(x) \amp =e^{-\frac{x}{3}} \,\, \text{and hence}\,\, f(2)=e^{-\frac{2}{3}} \\ f'(x) \amp =-\frac{1}{3}e^{-\frac{x}{3}} \,\, \text{and hence}\,\, f'(2)=-\frac{1}{3}e^{-\frac{2}{3}} \\ f''(x) \amp =\frac{1}{9}e^{-\frac{x}{3}} \,\, \text{and hence}\,\, f''(2)=\frac{1}{9}e^{-\frac{2}{3}} \end{align*}

Thus the second order approximation for \(f(x)=e^{-\frac{x}{3}} \) about \(x=2, \) (or the Taylor polynomial of degree \(2, \) for \(f(x)=e^{-\frac{x}{3}} \) about \(x=2\)), is

\begin{align*} T_{2}(x) \amp =e^{-\frac{2}{3}}-\frac{1}{3}e^{-\frac{2}{3}}(x-2)+\frac{1}{9}e^{-\frac{2}{3}}\dfrac{(x-2)^{2}}{2} \\ \amp =e^{-\frac{2}{3}}-\frac{1}{3}e^{-\frac{2}{3}}(x-2)+\frac{1}{18}e^{-\frac{2}{3}}(x-2)^{2} \end{align*}

Find the Taylor polynomial of degree \(4 \) for \(f(x)=x\cos(x) \) about \(x=\frac{\pi}{2}. \)

Answer.

\(T_{4}(x) = -\dfrac{\pi}{2} (x-\dfrac{\pi}{2}) - (x-\dfrac{\pi}{2})^2 + \dfrac{\pi}{2} \dfrac{(x-\dfrac{\pi}{2})^3}{3!} + \dfrac{(x-\dfrac{\pi}{2})^4}{3!}\)

Solution.

Since we already know the Taylor series for \(\cos(x) \) about \(x=\frac{\pi}{2} \) we can obtain the \(4^{\text{th}} \) degree Taylor polynomial for \(f(x)=x\cos(x) \) about \(x=\frac{\pi}{2} \) as follows

\begin{align*} f(x) \amp = x\cos(x) \\ \amp = (x-\frac{\pi}{2})\cos(x)+\frac{\pi}{2}\cos(x) \\ \amp = (x-\frac{\pi}{2}) \left[-(x-\frac{\pi}{2}) + \frac{(x-\frac{\pi}{2})^3}{3!} - \frac{(x-\frac{\pi}{2})^5}{5!} + \dots \right] + \frac{\pi}{2}\left[ -(x-\frac{\pi}{2}) + \frac{(x-\frac{\pi}{2})^3}{3!} - \frac{(x-\frac{\pi}{2})^5}{5!} + \dots \right] \\ \amp = \left[-(x-\frac{\pi}{2})^2 + \frac{(x-\frac{\pi}{2})^4}{3!} - \dots \right] + \left[ -\frac{\pi}{2}(x-\frac{\pi}{2}) + \frac{\pi}{2}\frac{(x-\frac{\pi}{2})^3}{3!} - \dots \right]. \end{align*}

Thus the \(4^{\text{th}} \) degree Taylor polynomial is

\begin{equation*} T_{4}(x) = -\frac{\pi}{2} (x-\frac{\pi}{2}) - (x-\frac{\pi}{2})^2 + \frac{\pi}{2} \frac{(x-\frac{\pi}{2})^3}{3!} + \frac{(x-\frac{\pi}{2})^4}{3!}. \end{equation*}

Exercises Example Tasks

1.

Find the Taylor series for \(f(x)=\ln(x). \) about \(x=e. \)

2.

Find the Taylor polynomial of degree \(3 \) for \(f(x)=\dfrac{1}{1-x} \) about \(x=2. \)

3.

Find the Taylor polynomial of degree \(4 \) for \(f(x)=x\ln(x) \) about \(x=e. \)

4.

Find the \(3\)rd degree Taylor polynomial for \(f(x)=x^2 e^{x} \) about \(x=1. \)

Remark 2.2.6. A little remark.

Computer algebra systems usually have commands for Taylor series. For example, here in Figure 2.2.7 is an example of a query to Wolfram Alpha that will work.

Figure 2.2.7.