Section 12.1 Homogeneous Second Order Linear DEs With Constant Coefficients
Example 12.1.1.
Guess solutions to the following homogeneous second order linear DEs with constant coefficients.
\(\displaystyle y''=0. \)
\(\displaystyle y''-y=0 \)
\(\displaystyle y(x)=Ax+B, \; A,B\in \mathbb{R}\)
\(\displaystyle y(x)=Ae^{x}+Be^{-x}, \; A,B\in \mathbb{R} \)
-
What function has its second derivative zero (i.e. has zero curvature)? Clearly any linear function satisfies this property and so we guess that the general solution to this DE is
\begin{equation*} y(x)=Ax+B, \; A,B\in \mathbb{R} \end{equation*} -
This DE can be rewritten as
\begin{equation*} y''=y. \end{equation*}The solution, then, is any function that has its second derivative equal to the function itself. This is a property of any of the exponential functions
\begin{equation*} y(x)=Ae^{x}. \end{equation*}It is also a property of the exponential functions
\begin{equation*} y(x)=Be^{-x}. \end{equation*}Thus every function of the form
\begin{equation*} y(x)=Ae^{x}+Be^{-x}, \; A,B\in \mathbb{R} \end{equation*}will be a solution to the DE.
Before looking at the method for solving a homogeneous second order linear DE with constant coefficients, i.e. a DE of the form
there are several things that we can predict about the solution, (based on Example 12.1.1 and previous lectures):
The general solution will be a family of functions involving two parameters.
The exponential function is a likely candidate for a solution.
Notice also that if both \(y_{1}(x) \) and \(y_{1}(x) \) are solutions to (12.1.1) then so will be \(y(x)=A y_{1}(x)+B y_{2}(x) \) where \(A \) and \(B \) are arbitrary constants. To see this, let \(y_{1}(x) \) and \(y_{2}(x) \) be solutions to (12.1.1), i.e.
Now let
Then
Substituting into (12.1.1) gives:
These observations, along with the following theorem, enable us to develop a method of solution for DEs of the form (12.1.1).
Theorem 12.1.2.
For the homogeneous second order linear DE
where \(P(x)\neq 0, \) given any pair of solutions \(y_{1}(x) \) and \(y_{2}(x) \) that are not constant multiples of each other a general solution to the DE is
Note: The proof of this theorem is beyond the scope of this course.
Example 12.1.3.
Given that \(y=e^{x},\; y=e^{-x}, \; y=\sinh(x), \text{ and } y=\cosh(x) \) are all solutions to the DE
write down a general solution to this DE.
From the above theorem, since none of these solutions are constant multiples of each other, any pair of them can be combined to form a general solution to the DE. Thus possible general solutions could be
and so on.
Recall that a general solution to the DE contains every solution to the DE. For example consider the particular solution
This solution belongs to the general solution \(y_{2}(x) \) with \(A=2 \; \text{and}\; B=-3. \) It also belongs to the general solution \(y_{1}(x) \) with \(A=-\frac{1}{2} \; \text{and}\; B=-\frac{5}{2}. \) and to the general solution \(y_{3}(x) \) with \(A=2 \; \text{and}\; B=-5. \)
Thus, initially at least, our method for trying to find the solutions to (12.1.1) is to try to find two different exponential functions that satisfy the DE and then combine them to obtain a general solution. To this end, let
where \(r \) is some, as yet unspecified, constant. Since \(y'=e^{rx}, \; \text{and}, y''=r^{2}e^{rx} \) for this to be a solution of (12.1.1) we have
Since \(e^{rx}\neq 0 \) for any value of \(r \) or \(x \) we conclude that (12.1.2) is a solution of (12.1.1) when
(12.1.3) is called the characteristic equation for a DE of the form of (12.1.1)).
If the characteristic equation (12.1.3)) has two real solutions (i.e. \(b^{2}-4ac>0 \)) then we are done since we will have found two solutions to (12.1.1) and, via the given theorem, we can combine these solutions to produce a general solution to (12.1.1). So if the solutions to the characteristic equation are \(r_{1} \) and \(r_{2} \) say, then the general solution to (12.1.1) is
Example 12.1.4.
Find the general solution to \(y''+3y'+2y=0. \)
\(y(x)=A e^{-x} + B e^{-2 x}.\)
The characteristic equation for this homogeneous second order linear DE with constant coefficients is
which has solutions
Thus the general solution to the DE is
If the characteristic equation (12.1.3) has only one real solution (i.e. \(b^{2}-4ac=0\)) then we will have found only one exponential solution to (12.1.1) , i.e.
To find a general solution we have to find another solution (that is not a constant multiple (12.1.1)). It turns out that another solution to (12.1.3) can be found by trying a function of the form
Differentiating \(y \) and substituting into (12.1.1) gives
Since \(ar^{2}+br+c=0, \; 2ar+b=0 \) and \(e^{rx}\neq 0, \) (12.1.5) is a solution when
Clearly \(f(x)=1 \) satisfies (12.1.6) but this just gives us solution (12.1.4). also satisfies (12.1.6) and gives us a solution that is not a constant multiple of (12.1.4). Thus a general solution to (12.1.1) will be
Example 12.1.5.
Find the general solution to \(y''-4y'+4=0. \)
\(y(x)=Ae^{2x} + Bxe^{2x}.\)
The characteristic equation for this DE is
which has only the one real solution
Thus the general solution to the DE is
The final case to consider is that the characteristic equation (12.1.3) has complex roots, say
Even though we are looking for real solutions, for the moment let us consider the "complex solutions"
Using Euler's formula
we can write these complex solutions as
Adding constant multiples of two solutions gives another solution. Now
and
which are both real. We can check that functions are indeed solutions to (12.1.1) and so we have found two real solutions to (12.1.1) that aren’t constant multiples of each other. Thus, in the case that the characteristic equation has complex roots the general solution to the DE is
Example 12.1.6.
Find the general solution to \(y''-4y'+13y=0. \)
\(y(x)=Ae^{2 x}\cos(3 x) + B e^{2 x}\sin(3 x).\)
The characteristic equation for this homogeneous second order linear DE with constant coefficients is
which has the complex solutions
Thus the general solution to the DE is
The above discussion can be summarised as follows.
Theorem 12.1.7.
To solve the homogeneous second order linear DE with constant coefficients
-
Find the roots of the characteristic equation
\begin{equation*} ar^{2}+br+c=0. \end{equation*} -
If the characteristic equation has two real roots \(r_1 \text{ and } r_{2}\) then the general solution to (12.1.7) is
\begin{equation*} y(x)=Ae^{r_{1}x} + Be^{r_{2}x}. \end{equation*} -
If the characteristic equation has a repeated real root \(r \) then the general solution to (12.1.7) is
\begin{equation*} y(x)=A e^{rx} + Bxe^{rx}. \end{equation*} -
If the characteristic equation has complex roots \(\alpha\pm i\beta \) then the general solution to (12.1.7) is
\begin{equation*} y(x)=A e^{\alpha x}\cos(\beta x) + B e^{\alpha x}\sin(\beta x). \end{equation*}
Given that the general solution to a second order DE has two arbitrary constants in order to find a particular solution it is necessary to give two conditions. In an initial-value problem the conditions given are the values of \(y \) and \(y' \) at the same value of \(x \text{,}\) usually \(x=0. \) In a boundary-value problem the conditions given are the values of \(y \) at two different values of \(x. \) Even when we have a general solution to the DE, it may not always be possible to satisfy a given set of boundary-value conditions.
Example 12.1.8.
Solve the initial-value problem
\(y(x) = \dfrac{12}{5} e^{-\frac{x}{4}} + \dfrac{3}{5} e^{x}.\)
The DE is a homogeneous second order linear DE with constant coefficients. The characteristic equation then is
Since this equation has two real solutions,
the general solution is
Thus
Using the initial conditions gives the equations.
Solving these simultaneously gives
Thus the solution to the initial-value problem is
This solution is shown in Figure 12.1.9. Note that since \(r_{1}=-\frac{1}{4} < 0 \) the term in the general solution associated with this root (i.e. \(\frac{12}{5} e^{-\frac{x}{4}} \)) decays as \(x\to \infty. \) On the other hand since \(r_{2}=1 > 0 \) the term in the general solution associated with this root (i.e. \(\frac{3}{5} e^{x} \)) grows as \(x\to \infty. \) 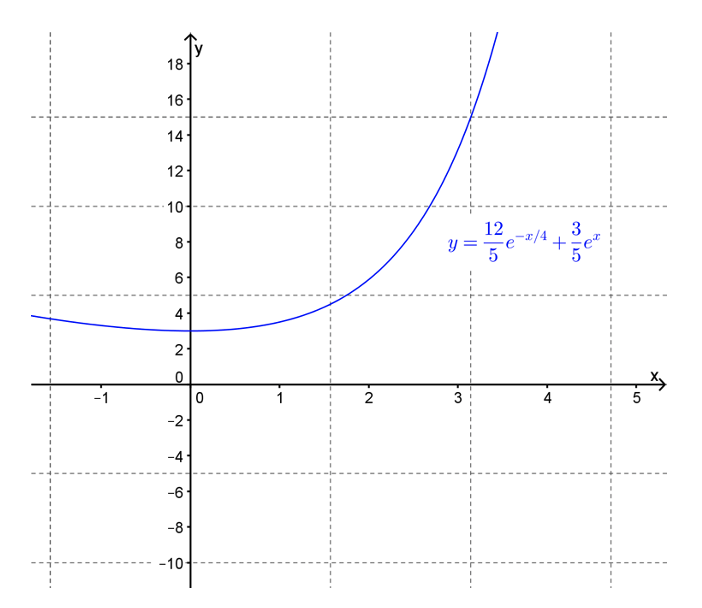
Example 12.1.10.
Solve the boundary-value problem
\(y(x)=e^{3x} ( \cos(4 x) + 2 e^{-\frac{3\pi}{8}} \sin(4 x)).\)
The characteristic equation is
which has the complex solutions
Thus the general solution is
Using the boundary conditions gives the equations
Thus the solution to the boundary-value problem is
This graph of this function is shown in Figure 12.1.11. Note that when the characteristic equation has complex roots, \(r=\alpha\pm\beta i\) the solutions the homogeneous second order linear DE with constant coefficients will be periodic in nature with frequency \(\beta\text{.}\) Further, if \(\alpha > 0\) then the oscillations will grow as \(x\to \infty \) whereas if \(\alpha < 0\) the oscillations will decay as \(x\to \infty. \) In this case \(\alpha =3\) and hence the oscillations increase in amplitude. 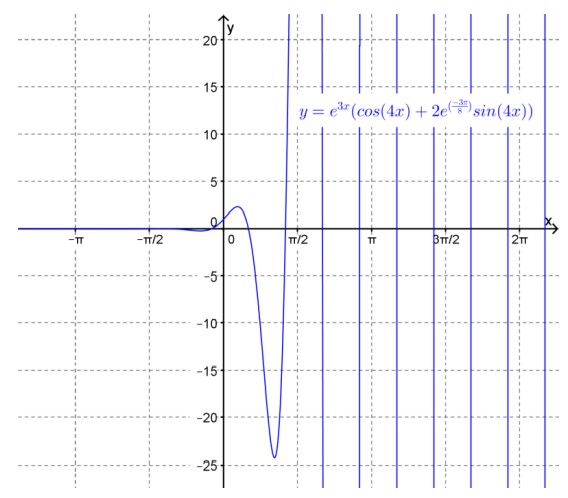
Exercises Example Tasks
1.
If \(x=x(t) \) find the solution to the initial-value problem
2.
Find the solution to the boundary-value problem
3.
Describe the long term behaviour of the solutions to the DE
4.
Use the substitution \(x=e^{z}. \) to solve the DE