Skip to main content

Section 17.4 Linear Transformations

There are many applications of matrices where we view the matrix as a transformation (or mapping) that takes one vector and transforms (or maps) it to another vector. So, if \(A\) is an \(m \times n\) matrix then \(A\) can be thought of as a transformation that takes the \(n \times 1\) vector \(x\) to the \(m \times 1\) vector \(\mathbf{b} = A\mathbf{x}\text{.}\)

Consider the matrix

\begin{equation*} A = \begin{pmatrix} 0 \amp 1 \\ 1 \amp 0\end{pmatrix}. \end{equation*}

Since \(A\) is a \(2 \times 2\) matrix, we can think of \(A\) as a transformation that takes each vector \(x\) in the plane to another vector in the plane, \(b = A\mathbf{x}\text{.}\) Under this transformation, for example, \(\mathbf{x} = \begin{pmatrix} 2 \\ 1 \end{pmatrix}\) goes to

\begin{equation*} \mathbf{b} = A\mathbf{x} = \begin{pmatrix} 0 \amp 1 \\ 1 \amp 0\end{pmatrix}\begin{pmatrix}2 \\ 1\end{pmatrix} = \begin{pmatrix}1 \\ 2\end{pmatrix} \end{equation*}

and \(\mathbf{x} = \begin{pmatrix} -1 \\ -4\end{pmatrix}\) goes to

\begin{equation*} \mathbf{b} = A\mathbf{x} =\begin{pmatrix} 0 \amp 1 \\ 1 \amp 0\end{pmatrix}\begin{pmatrix} -1\\ 4\end{pmatrix} = \begin{pmatrix} -4 \\ -1\end{pmatrix}. \end{equation*}

See Figure 17.4.2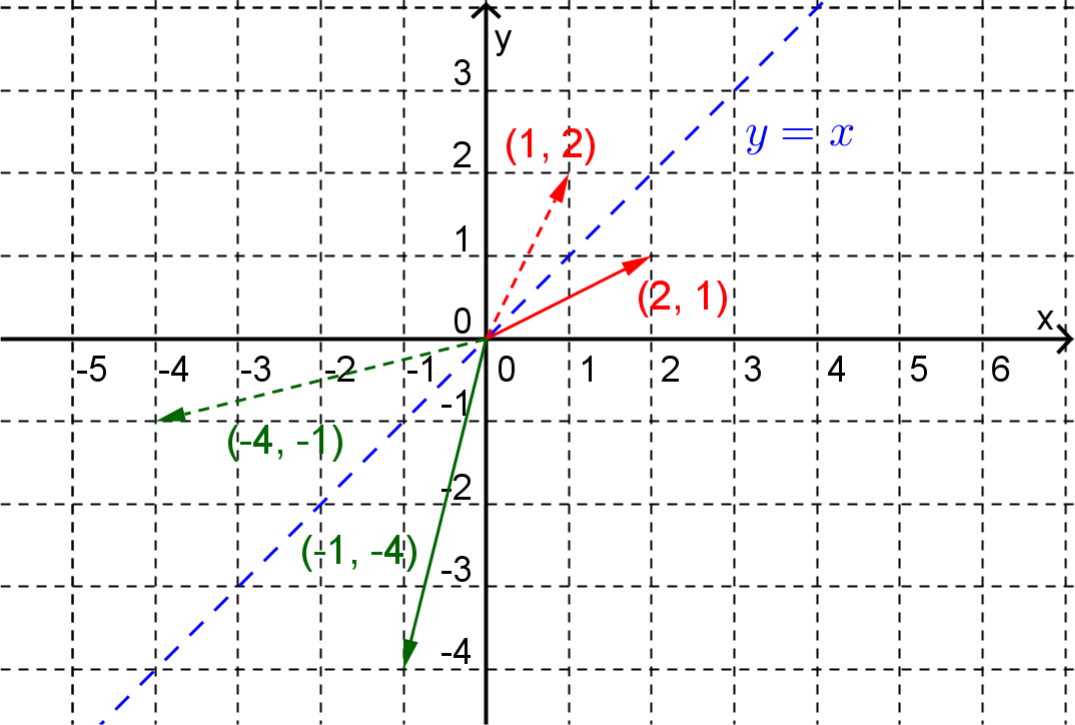

Figure 17.4.2.

In fact, \(A\) is the matrix for the transformation that we would describe as a reflection in the line \(y = x\text{.}\) To see this, let the vector \((x,y)\) be transformed to the vector \((b_1,b_2)\) under this reflection. Then we know that

\begin{align*} b_1 \amp = y = 0x +y \\ b_2 \amp = x = 1x + 0y \end{align*}

which we can write via matrices as

\begin{equation*} \mathbf{b} = \begin{pmatrix}b_1 \\ b_2 \end{pmatrix} = \begin{pmatrix} 0 \amp 1 \\ 1 \amp 0\end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix} = A\mathbf{x}. \end{equation*}

It can be shown that a rotation (in the plane) about the origin through angle \(\theta\) can be represented by the matrix

\begin{equation*} A = \begin{pmatrix} \cos(\theta) \amp -\sin(\theta) \\ \sin(\theta) \amp \cos(\theta)\end{pmatrix}. \end{equation*}

For example the matrix for a rotation about the origin through \(\pi^{c}\) (or \(180^{\circ}\)) is

\begin{equation*} A = \begin{pmatrix} -1 \amp 0 \\ 0 \amp -1 \end{pmatrix}. \end{equation*}

Determine the matrix for the transformation in which a reflection in the line \(y = x\) is followed by a rotation about the origin through \(\pi^c\text{.}\)

Answer.
\(\begin{pmatrix} 0 \amp -1 \\ -1 \amp 0\end{pmatrix}\)
Solution.

Let \(A_1 = \begin{pmatrix} 0 \amp 1 \\ 1 \amp 0\end{pmatrix}\) and \(A_2 = \begin{pmatrix} -1 \amp 0 \\ 0 \amp -1 \end{pmatrix}.\) Then, under the given transformation the vector \(\mathbf{x}\) will be mapped to the vector \(\mathbf{b}\) where

\begin{equation*} \mathbf{b} = A_2(A_1 \mathbf{x}) = (A_2A_1)\mathbf{x}, \end{equation*}

so the required matrix \(A\) can be found via matrix multiplication, i.e.,

\begin{equation*} A = A_2A_1 =\begin{pmatrix} -1 \amp 0 \\ 0 \amp -1 \end{pmatrix} \begin{pmatrix} 0 \amp 1 \\ 1 \amp 0\end{pmatrix} = \begin{pmatrix} 0 \amp -1 \\ -1 \amp 0\end{pmatrix}. \end{equation*}

Note that given that the matrix for a reflection in the line \(y = kx\) is

\begin{equation*} \begin{pmatrix} \dfrac{1-k^2}{1+k^2} \amp \dfrac{2k}{1+k^2}\\ \dfrac{2k}{1+k^2} \amp -\dfrac{1-k^2}{1+k^2} \end{pmatrix} \end{equation*}

we can see that the matrix \(A\) represents a reflection in the line \(y=-x\text{.}\)

Transformations that can be represented via a matrix are called linear transformations. When the matrix is a \(2 \times 2\) matrix the transformation is called a linear transformation of the plane.

Exercises Example Tasks

1.

Which vectors are mapped to \(\begin{pmatrix} 1 \amp 1 \amp 0 \end{pmatrix}^T\) under the transformation whose matrix is

\begin{equation*} \begin{pmatrix} 1 \amp 2 \amp -1 \\ 0 \amp -1 \amp 2 \\ 2 \amp 3 \amp 0 \end{pmatrix}\\text{.} \end{equation*}

2.

Find the matrix for the transformation of the plane in which a rotation about the origin through \(180^{\circ}\) is followed by a reflection in the line \(y = 2x\text{.}\)

3.

Find the vector to which \(\mathbf{x} = \begin{pmatrix}1 \\ 2\end{pmatrix}\) is mapped by \(\begin{pmatrix} 3 \amp 4 \\ 1 \amp 2 \end{pmatrix}\) followed by \(\begin{pmatrix}2 \amp 1 \\ 3 \amp 3 \end{pmatrix}\) followed by \(\begin{pmatrix}-1 \amp 1 \\ -1 \amp 0\end{pmatrix}.\)