Section 7.3 Global Extrema
Definition 7.3.1. Global Extrema.
Consider the function of two variables \(f(x,y)\) on the domain D.
If there exists some point \((x_0,y_0)\) in \(D\) such that \(f(x,y) \leq f(x_0,y_0)\) for all points \((x,y)\) in \(D\) then the function has a global maximum at \((x_0,y_0)\text{.}\)
Similarly, if there exists some point \((x_0,y_0)\) in \(D\) such that \(f(x,y) \geq f(x_0,y_0)\) for all points \((x,y)\) in \(D\) then the function has a global minimum at \((x_0,y_0)\text{.}\)
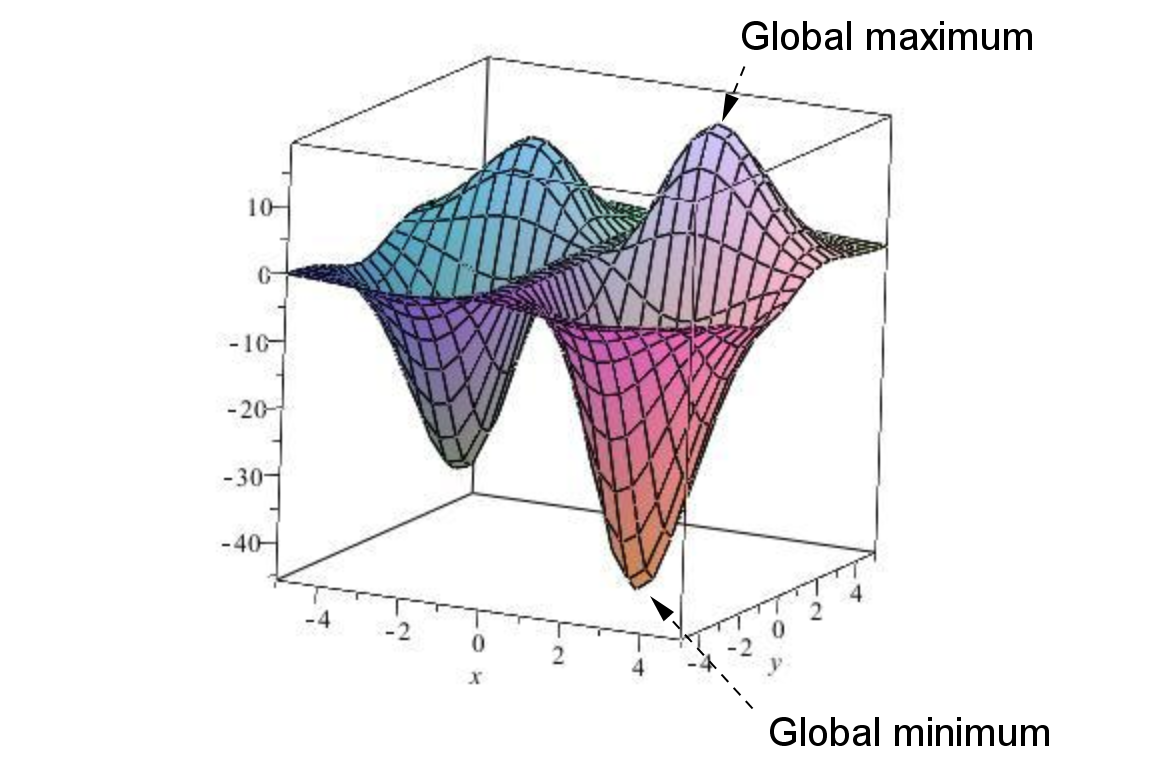
Example 7.3.2.
The graph of the function
over the domain \(D = \left \{ (x,y): -5 \leq x \leq 5, \, -5 \leq y \leq 5 \right \}\) is shown below.
Before discussing global extrema for functions of two variables, recall the situation for a function of one variable \(y=f(x)\text{.}\) If \(f(x)\) is continuous on the closed interval \(I=[a,b]\) then \(f(x)\) is guaranteed to have both a global maximum and a global minimum on \(I\text{.}\)
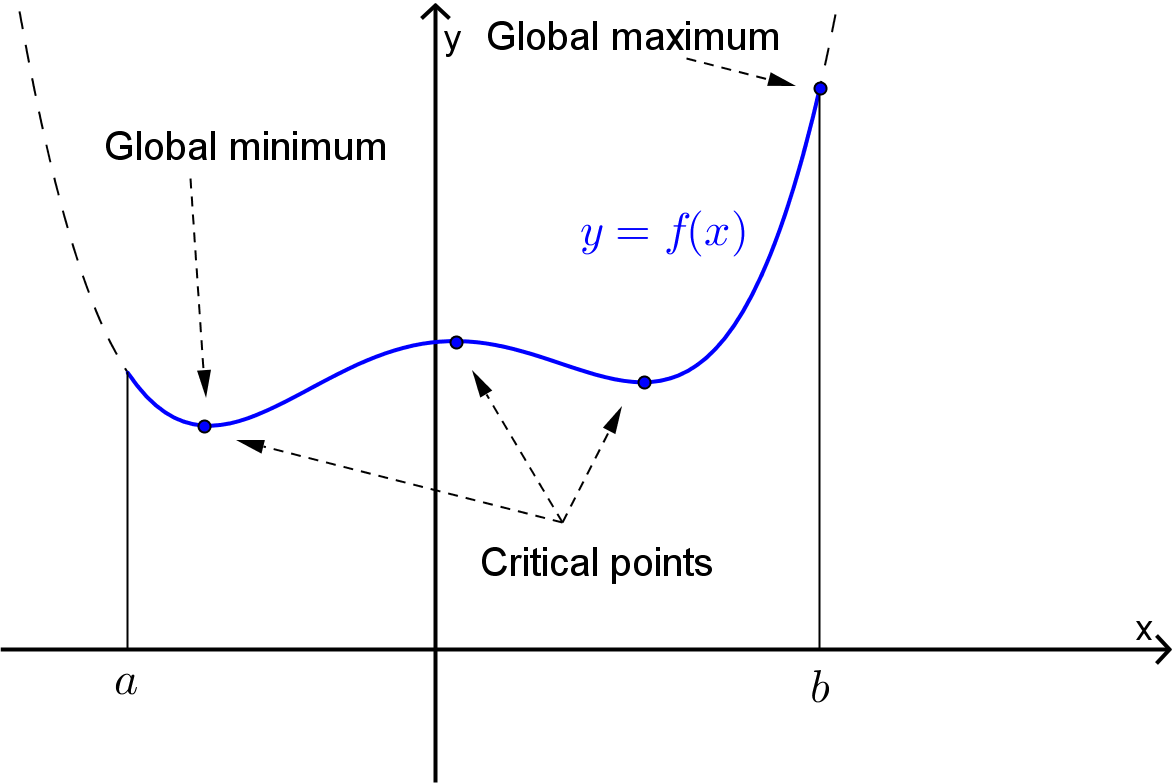
These global extrema can be found by evaluating \(f(x)\) at
All of the critical points of \(f(x)\) in \(I\text{,}\) and
The endpoints of \(L\text{.}\)
The procedure for finding the global extrema of functions of two variables is very similar and is based on the following theorem.
Theorem 7.3.5. Extreme Value Theorem.
If \(f(x,y)\) is a continuous function on the closed and bounded domain \(D \subset \mathbb{R}^2\) then \(f(x,y)\) has both a global maximum and a global minimum on \(D\text{.}\)
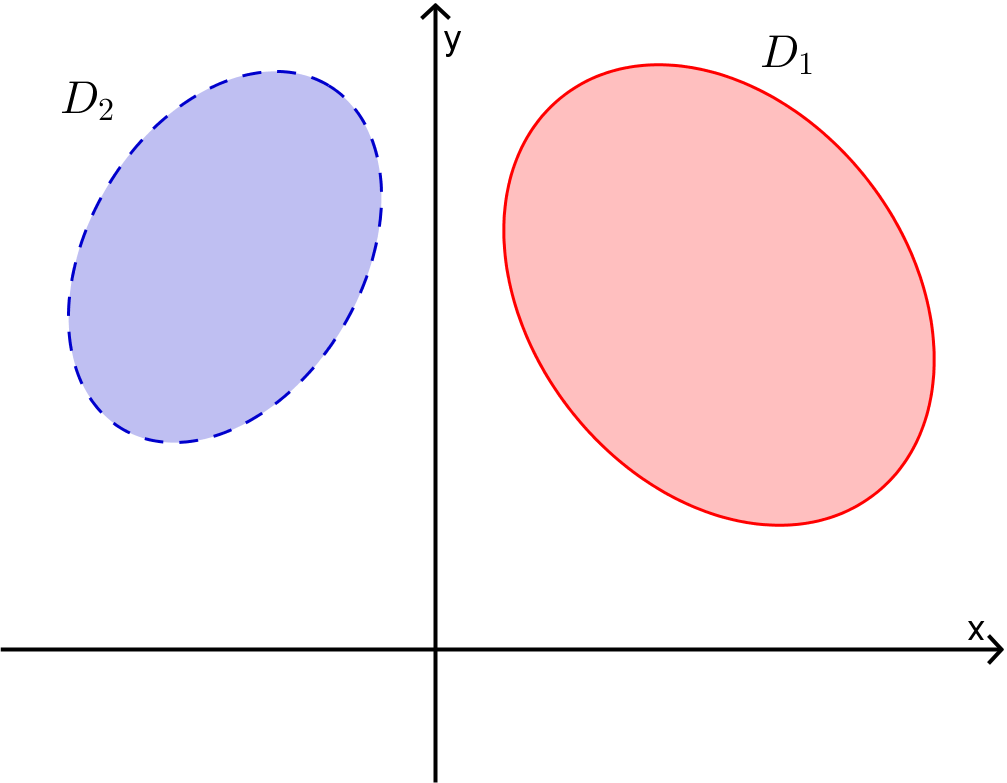
Note that a closed region, \(D \subset \mathbb{R}^2\text{,}\) is a region in the plane that contains its boundary. For example in the diagram below Region \(D_1\) would be a closed region whereas Region \(D_2\) is not closed.
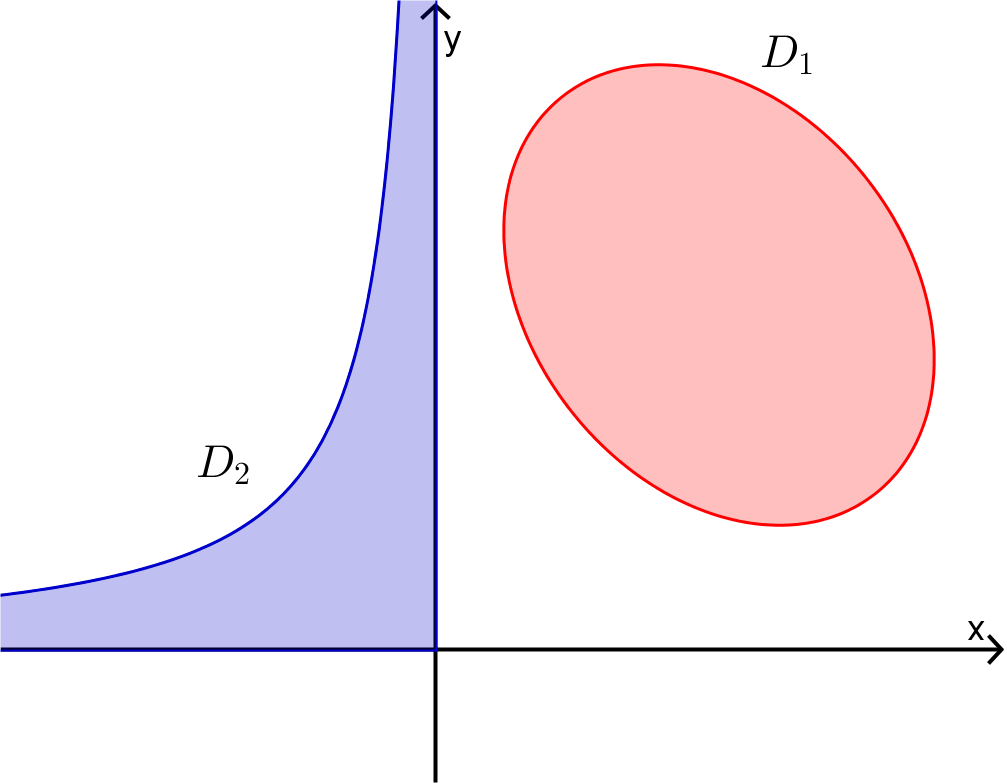
A bounded region, \(D \subset \mathbb{R}^2\text{,}\) is a region in the plane that doesn’t extend to infinity in any direction. For example in the diagram below Region \(D_1\) would be a bounded region whereas Region \(D_2\) is not bounded.
Remark 7.3.8. Locating Global Extrema.
To locate the global extrema of the continuous function \(f(x,y)\) on the closed and bounded domain \(D \subset \mathbb{R}^2\text{:}\)
Find all of the critical points in the interior of \(D\text{;}\)
Find the maximum and minimum values of \(f(x,y)\) on the boundary of \(D\text{;}\)
Evaluate \(f(x,y)\) at each of the above points and compare.
Example 7.3.9.
Find the global extrema of the function \(z(x,y) = x^2 + 2xy + 3y^2\) on the closed triangular region \(D\) with vertices \((-1,1)\text{,}\) \((2,1)\) and \((-1,-2)\text{.}\)
Global maximum: \(17\) at \((x,y) = (-1,2)\)
Global minimum: \(0\) at \((x,y)=(0,0)\text{.}\)
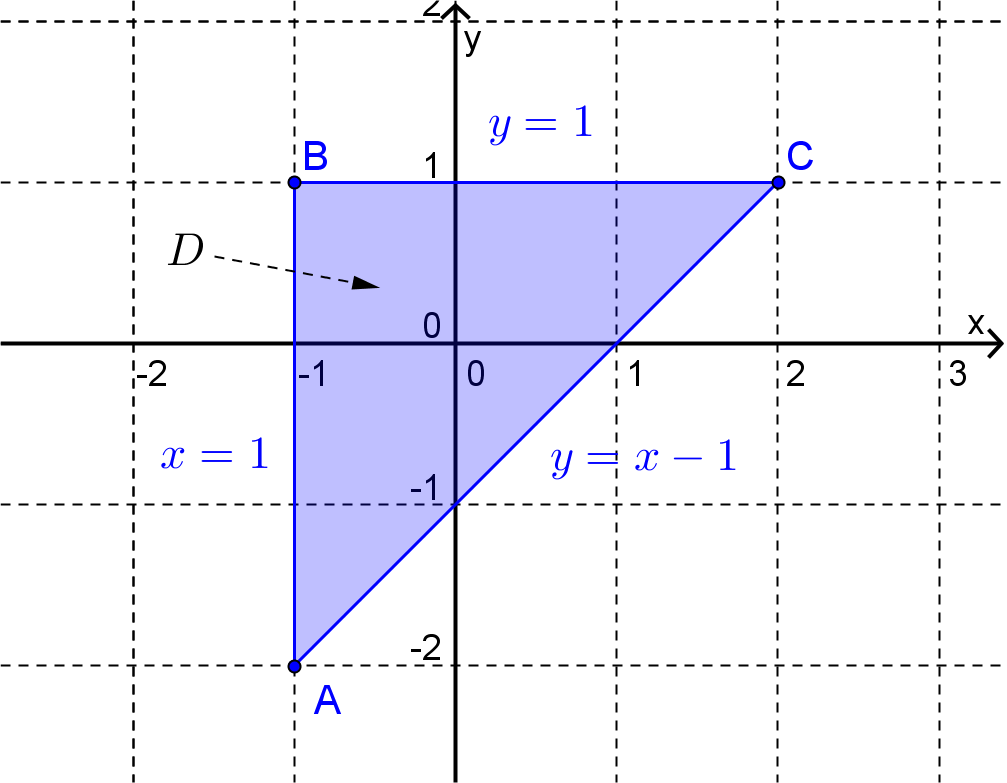
Firstly note that \(D\) is a closed and bounded region in the plane and so we can use the method outlined above. So begin by finding the critical points of \(z\text{.}\) Here
Critical points occur when \(z_x = z_y = 0\) and so this function has only one critical point at \((x,y) = (0,0)\text{.}\) This is inside \(D\) and so we evaluate the function at this point, i.e.
To find the maximum and minimum values of the function on the boundary we will have to consider the 3 sides of the triangle separately. Firstly, consider the side of the triangle defined by
On this interval we think of \(z\) as a function of \(x\) only, i.e.
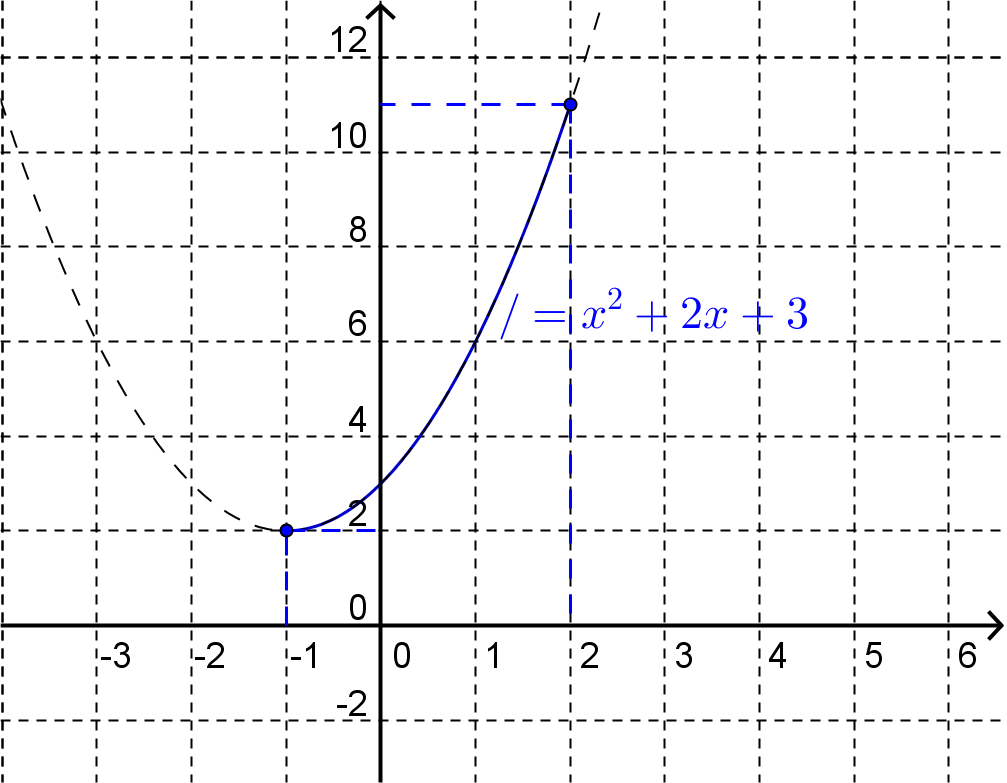
This has a maximum value \(11\) at \(x=2\) and minimum value \(2\) at \(x=-1\text{.}\)
Next consider the side of the triangle defined by
On this interval we think of \(z\) as a function of \(y\) only, i.e.
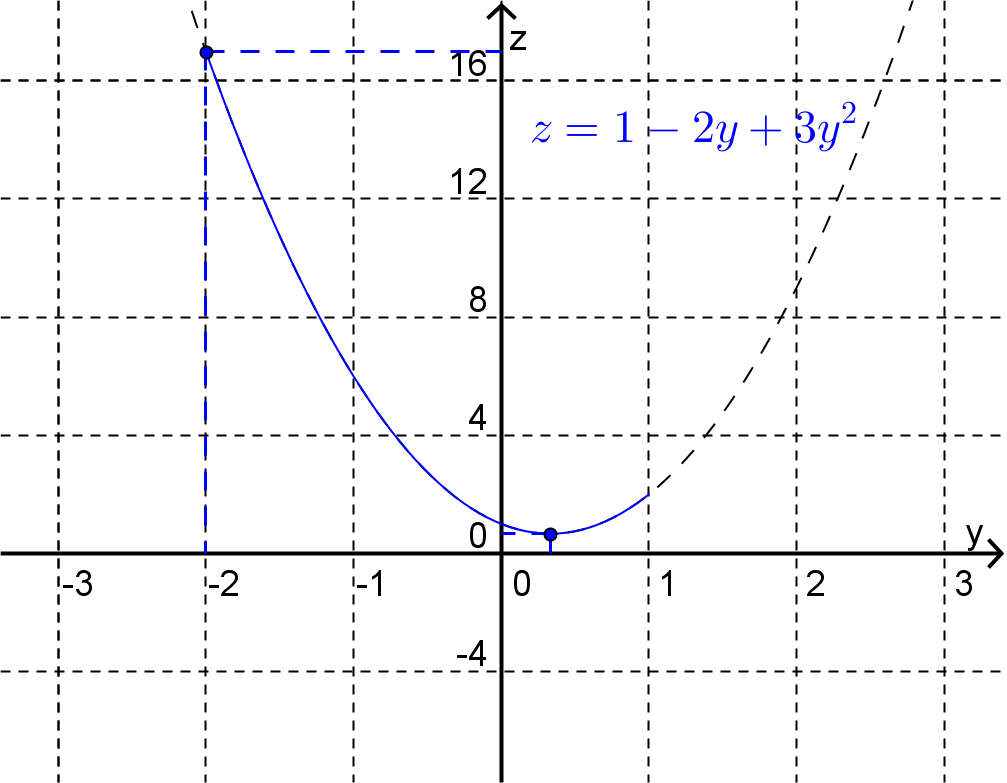
Again, using the technique given above for locating the global extrema for a function of one variable (or by looking at the graph) we find that the largest value of \(z\) occurs at \(y=-2\) (giving \(z=17\)) and the smallest value of \(z\) occurs at \(y=1/3\text{,}\) (giving \(z=2/3\)).
Finally on the interval defined by
we can think of \(z\) as a function of \(x\) only, i.e.
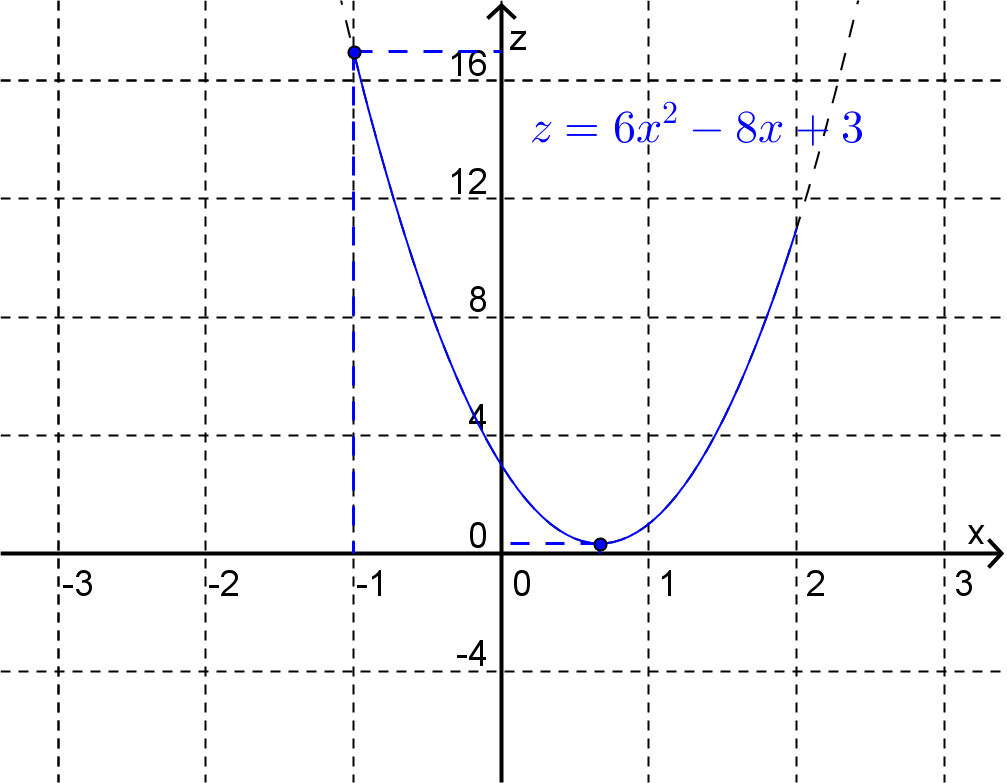
For this function the global maximum is \(17\) at \(x=-1\) and the global minimum is \(1/3\) at \(x=2/3\text{.}\)
On comparing the value of the function \(z(x,y) = x^2 + 2xy + 3y^2\) at each of the global extrema on the sides of the triangle and at the critical point inside the region we conclude that the function has a global maximum of \(17\) at \((x,y) = (-1,2)\) and a global minimum of \(0\) at \((x,y)=(0,0)\text{.}\)
Exercises Example Tasks
1.
Find the global extrema of \(z=2x^2 + x +y^2 - 2\) on \(D = \left \{ (x,y): x^2+y^2 \leq 4 \right \}\text{.}\)
2.
Find the global extrema of \(R(x,y) = x \sqrt{8-x^2-y^2}\) on \(D = \left \{ (x,y): x^2+y^2 \leq 8 \right \}\text{.}\)