Section 3.1 Functions of Two Variables
In Math1110 we studied "(real valued) functions of one variable", that is functions of the form,
where \(D\subseteq\mathbb{R}\) is called the domain. We used the notation \(y=f(x)\) to denote such functions where \(x\) denotes the independent variable and \(y\) the dependent variable.
We have seen that functions of one variable are useful in practice but (of course) there are many real world relationships that are more complicated and can't be well modelled by these functions.
Example 3.1.1.
Suppose that we have a thin metal plate and that we are interested in the temperature \(T\) on this plate. In general the temperature will vary from point to point. If we imagine a coordinate grid on the plate then points on the plate can be identified by their coordinates \((x,y)\text{.}\) Thus \(T\) will depend on two independent variables, \(x\) and \(y\text{.}\) Thus we would write
and say that \(T\) is a function of two variables.
Note that functions of two variables are of the form
where \(D\subseteq\mathbb{R}^2\) is again the domain. Formally, we define a function of two variables as:
Definition 3.1.2.
A (real valued) function \(f\) of two variables is a rule that assigns to each ordered pair of real numbers \((x,y)\) in a set \(D\) a unique (real) number denoted by \(f(x,y)\text{.}\)Thus,
are examples of functions of two variables.
The set \(D\) is called the domain of the function. Unless specified otherwise, we take \(D\) to be the largest possible set of ordered pairs for which we can calculate \(f\text{.}\) The range of \(f\) is the associated set of values that \(f\) takes on.
Example 3.1.3.
Consider the function \(f(x,y)=\ln(x-y-1)\text{.}\)
Find the domain of \(f\)
Find:
\(\displaystyle f(3,1)\)
\(\displaystyle f(\frac{1}{2},-\sqrt{5})\)
\(\displaystyle f(1,3)\)
\(\displaystyle D=\{(x,y):y \lt x-1\}\)
\(\displaystyle f(3,1)=0\)
\(f(\frac{1}{2},-\sqrt{5})=0.5516\) (to 4.d.p.).
\(f(1,3)\) is not defined.
-
Since the argument of the log function has to be positive, the domain \(D\) is the set of points in the plane satisfying
\begin{equation*} D=\{(x,y):y \lt x-1\} \end{equation*}
\(\displaystyle f(3,1)=\ln(3-1-1)=\ln(1)=0\)
\(f(\frac{1}{2},-\sqrt{5})=\ln(\frac{1}{2}+\sqrt{5}-1)=\ln(\sqrt{5}-\frac{1}{2})=0.5516\) (to 4.d.p.).
Since \((1,3)\) is not in the domain of \(f\text{,}\) \(f(1,3)\) is not defined.
Example 3.1.4.
Consider the function \(f(x,y)=y-xy\)
Find the domain of \(f\)
Find:
\(\displaystyle f(3,1)\)
\(\displaystyle f(\frac{1}{2},-\sqrt{5})\)
\(\displaystyle f(1,3)\)
\(\displaystyle \mathbb{R}^2\)
\(\displaystyle f(3,1)=-2\)
\(\displaystyle f(\frac{1}{2},-\sqrt{5})=-\frac{\sqrt{5}}{2}\)
\(\displaystyle f(1,3)=0\)
Since we can calculate \(f\) for all values of \(x\) and \(y\) the domain of \(f\) is \(\mathbb{R}^2\)
\(\displaystyle f(3,1)=1-3\times 1=-2\)
\(\displaystyle f(\frac{1}{2},-\sqrt{5})=-\sqrt{5}+\frac{1}{2}\times\sqrt{5}=-\frac{\sqrt{5}}{2}\)
\(\displaystyle f(1,3)=3-1\times 3=0\)
The graph of a function of two variables is a surface in \(\mathbb{R}^3\) which passes the vertical line test. In general it is hard to draw the graph of a function of two variables by hand and so usually we get a computer to do it. The following plots have been done using the specialist mathematical software Maple but Wolfram Alpha will produce such plots too.
Example 3.1.5.
Produce the graph of the function \(z=f(x,y)=x^2+y^2\)
Solution.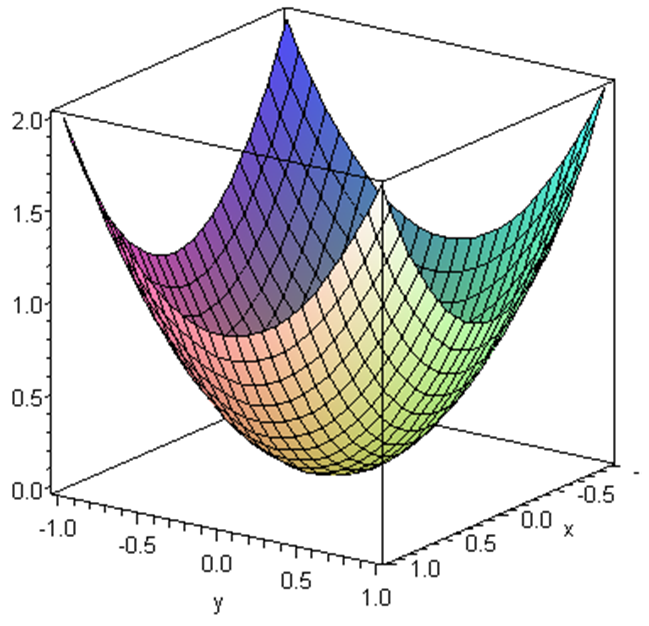
Example 3.1.7.
Produce the graph of the function \(f(x,y)=x(3y-2)(5x+2)e^{-(x^2+y^2)/5}\)
Solution.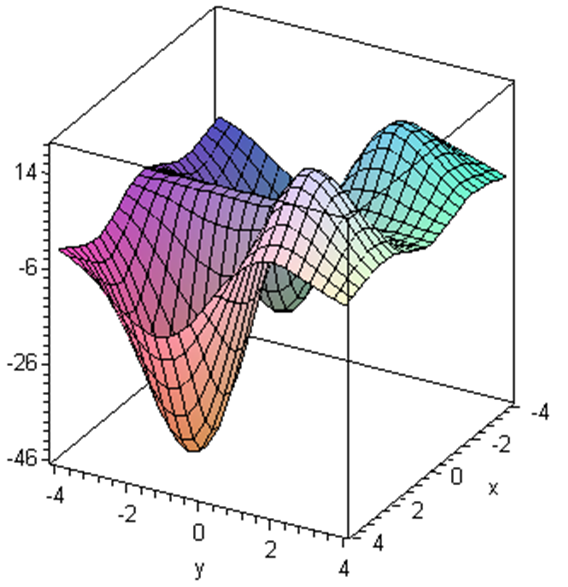
Example 3.1.9.
Produce the graph of the function \(f(x,y)=\sqrt{x^2+y^2}e^{-(x^2+y^2)}\)
Solution.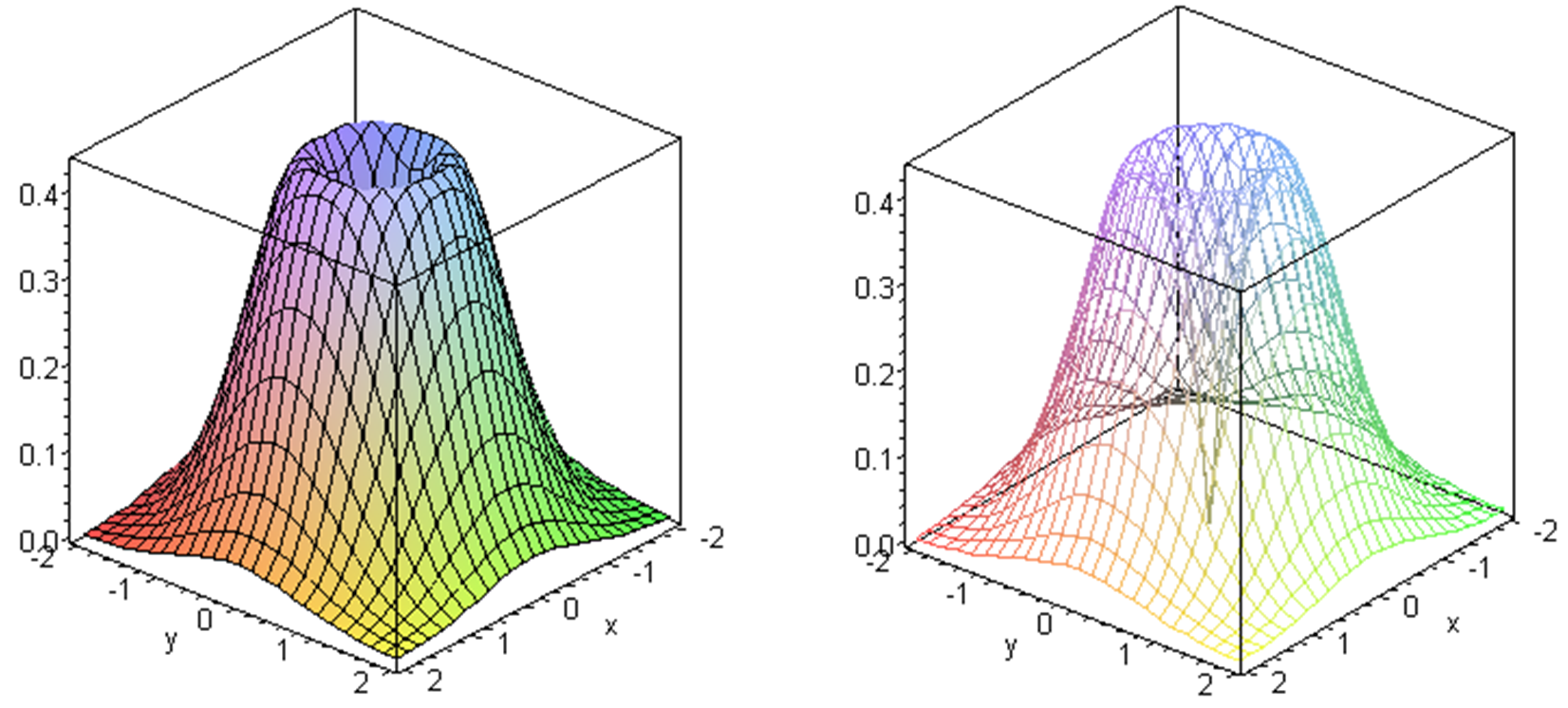
Not all surfaces in \(\mathbb{R}^3\) represent the graph of a function of two variables.
Example 3.1.11.
The surface associated the equation \(x^2+y^2+z^2=4\) is a sphere of radius \(2\) and whose centre is the origin. Clearly this surface does not pass the vertical line test. For example, when \((x,y)=(0,0)\text{,}\) \(z\) could be either \(+2\) or \(-2\text{.}\) 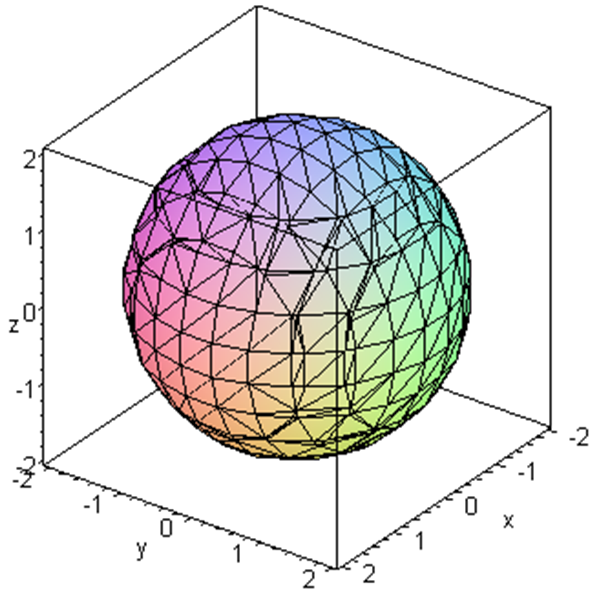
Exercises Example Tasks
1.
Determine the domain of the function \(f(x,y)=\dfrac{\sin(y)}{xy-1}\text{.}\)
2.
Sketch the graph of the following functions.
\(\displaystyle f(x,y)=3\)
\(\displaystyle f(x,y)=-x-2y+2\)
3.
Sketch the surface associated with the equation \(f(x,y)=x^2+y^2-4\text{.}\) Could the surface be the graph of a function of two variables?