Skip to main content

Section 3.3 Surfaces of Revolution

The surface associated with the graph of \(f(x,y)=\sqrt{x^2+y^2}e^{-(x^2+y^2)}\) (see Example 3.1.9) is an example of a special kind of surface...a surface of revolution.

Definition 3.3.1.

A surface of revolution is a surface in \(\mathbb{R}^3\) obtained by rotating a curve about an axis.

Determine the equation of the surface obtained by rotating the curve in the \(xz\)-plane \(z=2-3x, x\geq 0\) about the \(z\)-axis.

Answer.

\(f(x,y)=2-3\sqrt{x^2+y^2}\)

Solution.

Figure 3.3.3.
Let the equation of the surface be \(z=f(x,y)\text{.}\) Then the equation of the level curves of the surface will be

\begin{equation*} f(x,y)=k \end{equation*}

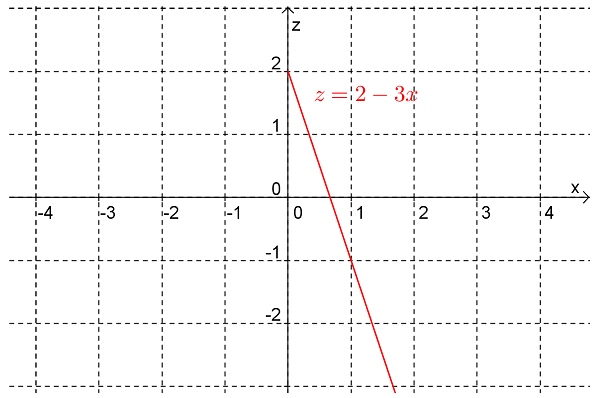
Now, note that the cross-sections of the surface of revolution perpendicular to the \(z\)-axis (i.e. the level curves) will be circles. For example the cross section at \(z=k\) will be a circle with centre \((0,0)\) and radius \(\frac{2-k}{3}\) and hence has equation

\begin{equation*} x^2+y^2=\left(\frac{2-k}{3}\right)^2 \end{equation*}

On re-arranging this equation we obtain

\begin{equation*} k=2-3\sqrt{x^2+y^2} \end{equation*}

Putting this into \(f(x,y)=k\) gives

\begin{equation*} f(x,y)=2-3\sqrt{x^2+y^2} \end{equation*}

On repeating what we did in the above example in general gives:

Definition 3.3.4.

The equation of a surface of revolution obtained by rotating the curve \(z=f(x), x\geq 0\) in the \(xz\)-plane about the \(z\)-axis will be
\begin{equation*} z=f(\sqrt{x^2+y^2}) \end{equation*}

Determine the equation of the surface obtained by rotating the curve in the \(xz\)-plane

\begin{equation*} z=xe^{-x^2}, x\geq 0 \end{equation*}

about the \(z\)-axis.

Answer.

\(z=\sqrt{x^2+y^2}e^{-(x^2+y^2)}\)

Solution.

Figure 3.3.6.
The equation of the surface of revolution will be

\begin{equation*} z=f(\sqrt{x^2+y^2}) \textrm{ where } f(x)=xe^{-x^2} \end{equation*}

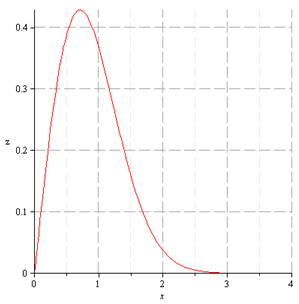
that is,

\begin{equation*} z=\sqrt{x^2+y^2}e^{-\left(\sqrt{x^2+y^2}\right)^2}=\sqrt{x^2+y^2}e^{-(x^2+y^2)} \end{equation*}

Is the graph of \(f(x,y)=4-x^2-y^2\) a surface of revolution?

Solution.

Since we can write the function as

\begin{equation*} f(x,y)=4-\left(\sqrt{x^2+y^2}\right)^2 \end{equation*}

this surface can be obtained by rotating the curve in the \(xz\)-plane

\begin{equation*} z=4-x^2, x\geq 0 \end{equation*}

Exercises Example Tasks

1.

Determine the equation of the surface obtained by rotating the curve \(z=\sqrt{4-x^2}, x\geq 0\) about the \(z\)-axis. Make a sketch of the surface.

2.

Is the graph of \(f(x,y)=xy^2-y^3\) a surface of revolution?