Section 10.1 First Order Separable DEs
Definition 10.1.1.
A differential equation of the form
where \(g(y)\neq 0\) is called a first order separable DE.
Example 10.1.2.
Which of the following DEs are first order separable DEs?
\(\displaystyle y^2y'=x \)
\(\displaystyle y''+2y=0 \)
\(\displaystyle \frac{dy}{dt}+3e^t=ye^t \)
\(\displaystyle \frac{dy}{dt}+ty=2 \)
\(\displaystyle y'=y(1-y) \)
\(\displaystyle y'=y(x-y) \)
\(a\text{,}\) \(c\) and \(e\)
This DE can be written as
\begin{equation*} y'=\frac{x}{y^2} \end{equation*}Thus it is a first order separable DE with \(f(x)=x\) and \(g(y)=\frac{1}{y^2}\text{.}\)This DE is a second order DE (due to the \(y''\) term) and hence cannot be a first order separable DE.
This DE can be rearranged as
\begin{equation*} \frac{dy}{dt}=e^t(y-3) \end{equation*}and hence is a first order separable DE with \(f(t)=e^t\) and \(g(y)=y-3\text{.}\)When we try to rearrange this DE in the same manner as we did in part (c) we obtain
\begin{equation*} \frac{dy}{dt}=2-ty \end{equation*}This is not of the form \(y'=f(t)g(y)\) and hence this first order DE is not separable.This DE is already in the form of a first order separable DE with \(f(x)=1\) and \(g(y)=y(1-y)\text{.}\)
The right hand side of this DE can't be rearranged into the form \(y'=f(x)g(y)\) and so this DE is not a first order separable DE.
The method for solving first order separable DEs is based on integration by substitution. This integration technique was covered in Math1110 but the following example is given as a reminder.
Example 10.1.3.
Evaluate the integral \(\displaystyle\int 2x\sin(x^2) \hspace{2mm} dx\text{.}\)
Answer.\(\displaystyle\int 2x\sin(x^2)\hspace{2mm} dx=-\cos(x^2)+C\)
Since the integrand is of the form \(g'(x)\sin(g(x))\) (or, in Leibniz notation \(\sin(g(x))\frac{dg}{dx}\)) make the substitution
Then
In general, the integration by substitution method says that for an integral of the form
the substitution
transforms the integral to
More succinctly, we can write this as
(As an aside, we saw in Math1110 that this formula follows directly from the chain rule of differentiation.)
Returning now to the problem of solving first order separable DEs, i.e. to solving DEs of the form
Assuming that \(g(y)\neq 0\text{,}\) rearrange the DE as
Note that in this step we are "separating the variables". Now integrate both sides with respect to \(x\) to obtain
Using the integration by substitution formula on the left hand side gives
So long as we can actually perform the integrals on both sides of this equation we will have an equation which will implicitly define \(y\) (the unknown function) in terms of \(x\) (the independent variable). If we can further make \(y\) the subject of this equation then we will have found an explicit formula for the solution to the separable DE.
Example 10.1.4.
Find the general solution to the DE
\(y(x)=\dfrac{1}{2x^2+C}, \hspace{5mm} y(x)=0 \hspace{5mm} \textrm{ for } C\in\mathbb{R}\)
This is a first order separable DE so begin by separating the variables, i.e.
Now integrate both sides with respect to \(x\text{,}\)
Using the integration by substitution formula this becomes
Evaluating the integrals on both sides (and combining the two constants of integration) gives
Here we can make \(y\) the subject of the resulting equation and hence
Note that we can check whether this function is a solution to the DE by substituting back into the original DE. On the left hand side, using the chain rule to differentiate \(y\) we obtain
On the right hand side
and so \(y\) does indeed satisfy the DE.
The working so far has assumed that \(y^2\neq 0\) and hence that \(y\neq 0\text{.}\) Thus to check that we have found all of the solutions to the DE we must check whether the function \(y(x)=0\) is also a solution. Clearly it is. Thus the set of all solutions to the DE is
See Figure 10.1.5 for a sketch of these solutions for various values of \(C\text{.}\) 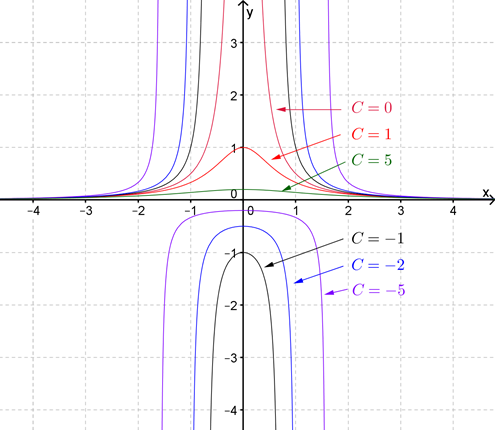
Example 10.1.6.
Find the solution to the initial-value problem
\(2y^2-\sin(y)=t^3\)
This is a first order separable DE so begin by separating the variables, i.e.
Integrating both sides with respect to \(t\) and applying the integration by substitution formula to the left hand side gives
Evaluating the integrals on both sides (and combining the two constants of integration) gives
We can't make \(y\) the subject of this equation and so in this case we can't find an explicit formula for the general solution to the DE. Substituting the initial condition into the implicit equation gives
i.e.
Thus the solution to the initial-value problem is the relevant function \(y(t)\) defined implicitly by
The curve defined implicitly by this equation is shown in Figure 10.1.7 and from this we can see that the "bottom" part of the curve will be the function that is the solution to the initial-value problem. 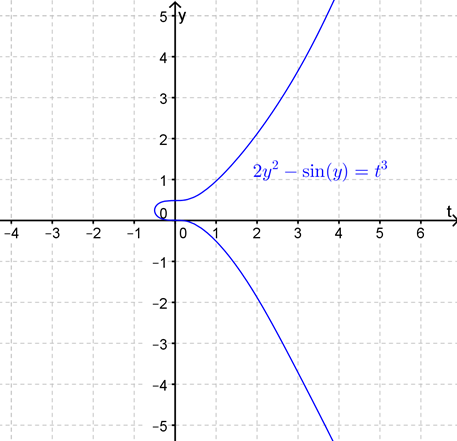
Example 10.1.8.
Find the general solution to the DE
Note: We looked at this example in Chapter 9. There we sketched a direction field for the DE.
Answer.\(y(x)=\dfrac{Ae^x}{1+Ae^x}\)
This is a first order separable DE with \(f(x)=1\) (i.e. it is autonomous) and \(g(y)=y(1-y)\text{.}\) On separating the variables and integrating both sides with respect to \(x\) we obtain
To evaluate the integral on the left hand side we have to use partial fraction decomposition, by which we can determine that
Thus
This can be rearranged as
Figure 10.1.9 shows this curve when \(A=1\) superimposed on top of the direction field for the DE. Also shown in the figure are the solutions \(y(x)=0\) and \(y(x)=1\) which come from checking separately the cases where \(g(y)=0\text{.}\) 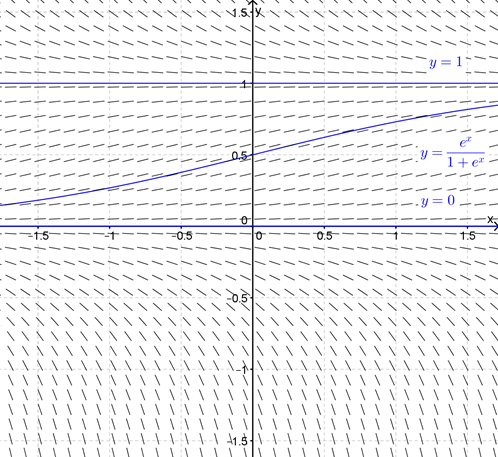
Example 10.1.10.
Find the solution to the initial-value problem
Note: We looked at this example in section Chapter 9 where we used Euler’s method with \(\Delta x=0.1\) to approximate the value of the solution at \(x=0.3\text{.}\)
Answer.\(y(x)=2e^{x^2/2}-1\)
This is a first order separable DE with \(f(x)=x\) and \(g(y)=y+1\text{.}\) On separating the variables and integrating both sides with respect to \(x\) we obtain
Evaluating the integrals and rearranging gives
To satisfy the initial condition
Note: From this solution
The Euler method approximation was
Figure 10.1.11 shows both the analytic solution and the Euler approximation over the domain \(0\leq x\leq 0.3\text{.}\) 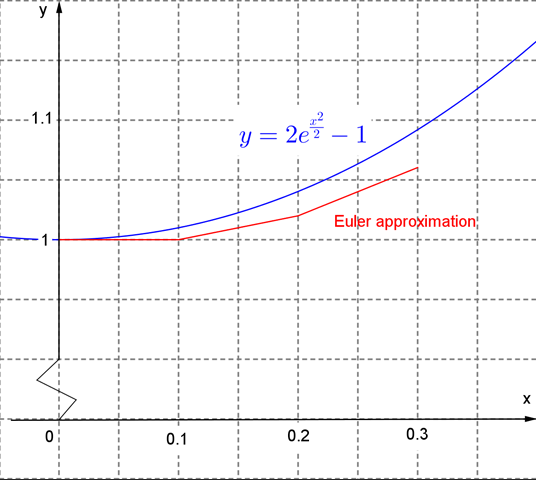
Exercises Example Tasks
1.
Find the general solution to the DE
2.
Solve the initial-value problem