Interpretation Via Rows

Section 16.1 Interpretation Via Rows

We know that a linear equation in two variables can be interpreted as the equation of a line in the plane. For example the equation

2 x + 3 y = 6

🔗

can be interpreted as a line of slope

- \frac{2}{3}

and with a

y

-intercept of

2 .

Thus, for a system of linear equations involving two variables each row can be interpreted as a line in the plane and finding the solution to this system can be thought of as finding all of those points in the plane (if any) that lie on all of the lines. (We had several examples last week where we interpreted systems involving just two linear equations this way.)

🔗

Example 16.1.1.

Solve the following system of linear equations and interpret the result geometrically.

\begin{aligned} 2 x + 3 y & = 6 \\ - x + 2 y & = 2 \\ 3 x - 2 y & = - 3 \end{aligned}

Solution.

Forming the augmented matrix and row reducing it to reduced row-echelon form gives

(\begin{matrix} 2 & 3 & 6 \\ - 1 & 2 & 2 \\ 3 & - 2 & - 3 \end{matrix}) \sim (\begin{matrix} 1 & 0 & \frac{6}{7} \\ 0 & 1 & \frac{10}{7} \\ 0 & 0 & - \frac{19}{7} \end{matrix})

We can see from the reduced row-echelon form that this system of equations is inconsistent. The geometric interpretation of this is that there is no point in the plane that lies on all three lines, as can be seen in Figure 16.1.2.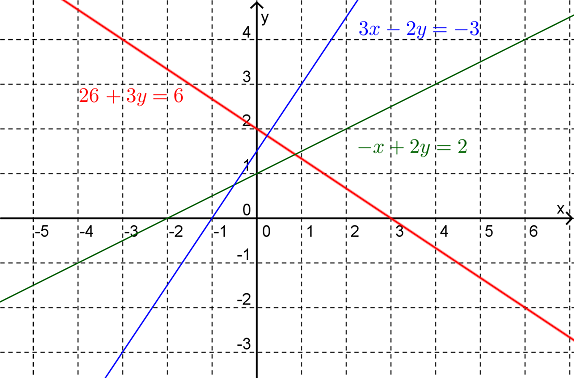

🔗

For systems of linear equations involving three unknowns each equation (or alternatively each row in the augmented matrix) can be thought of as representing a plane in

R^{3},

i.e. in three dimensions. Recall that the Cartesian equation of the plane that is normal to the vector

n = ⟨ a, b, c ⟩

and passes through the point

(x_{0}, y_{0}, z_{0})

a x + b y + c z = k where k = a x_{0} + b y_{0} + c z_{0}

🔗

i.e. a linear equation in three variables. Thus the solution to a system of linear equations in

3

variables can be interpreted as those points in

R^{3}

(if any) that lie on all of the planes in the system.

🔗

Example 16.1.3.

Solve the following system of linear equations and interpret your answer geometrically (in terms of the rows).

\begin{aligned} x_{1} + 2 x_{2} + 3 x_{3} & = - 3 \\ 4 x_{1} + 3 x_{2} + 2 x_{3} & = 8 \\ - x_{1} + 3 x_{2} + 7 x_{3} & = - 17 \end{aligned}

Solution.

Forming the augmented matrix and row reducing it to reduced row-echelon form gives

(\begin{matrix} 1 & 2 & 3 & - 3 \\ 4 & 3 & 2 & 8 \\ - 1 & 3 & 7 & - 17 \end{matrix}) \sim (\begin{matrix} 1 & 0 & - 1 & 5 \\ 0 & 1 & 2 & - 4 \\ 0 & 0 & 0 & 0 \end{matrix})

From the reduced row-echelon form we can see that the solution set is

(x, y, z) = (5 + t, - 4 - 2 t, t), t \in R

The geometric interpretation of this solution, as shown in Figure 16.1.4, is that the $3$ planes intersect in the line with vector equation

(x, y, z) = (5, - 4, 0) + t (1, - 2, 1)

i.e. the line passing through the point $(5, - 4, 0)$ and parallel to the vector $(1, - 2, 1)$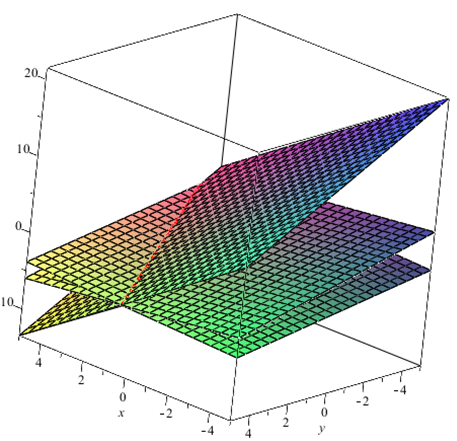

🔗

A linear equation in more than

n

variables (where

n > 3

) is said to represent an “

n

-dimensional hyperplane”. The geometric interpretation (in terms of rows) of the solution to a system of linear equations involving such equations would be the set of

n

-dimensional points that lie on all of the hyperplanes. Obviously drawing pictures for such systems is not possible.

🔗

Exercises Example Tasks

🔗

1.

What would you expect the reduced row-echelon form of the augmented matrix associated with the system of equations for $4$ lines in space meeting a point to look like.

🔗

2.

Solve the following system of linear equations and interpret your answer geometrically (in terms of the rows).

\begin{aligned} x_{1} + 2 x_{2} + 3 x_{3} & = 4 \\ 4 x_{1} + 3 x_{2} + 2 x_{3} & = 1 \\ 2 x_{1} + 3 x_{2} + 4 x_{3} & = 1 \end{aligned}

🔗

3.

What form would you expect the reduced row-echelon form of the augmented matrix associated with the system of equations for $3$ distinct parallel planes to take.